Chapter 13 The Western Collaborative Group Study
13.1 The Western Collaborative Group Study (wcgs) data set
Vittinghoff et al. (2012) explore data from the Western Collaborative Group Study (WCGS) in great detail9. We’ll touch lightly on some key issues in this Chapter.
# A tibble: 3,154 x 22
id age agec height weight lnwght wghtcat bmi sbp lnsbp dbp
<int> <int> <fct> <int> <int> <dbl> <fct> <dbl> <int> <dbl> <int>
1 2343 50 46-50 67 200 5.30 170-200 31.3 132 4.88 90
2 3656 51 51-55 73 192 5.26 170-200 25.3 120 4.79 74
3 3526 59 56-60 70 200 5.30 170-200 28.7 158 5.06 94
4 22057 51 51-55 69 150 5.01 140-170 22.1 126 4.84 80
5 12927 44 41-45 71 160 5.08 140-170 22.3 126 4.84 80
6 16029 47 46-50 64 158 5.06 140-170 27.1 116 4.75 76
7 3894 40 35-40 70 162 5.09 140-170 23.2 122 4.80 78
8 11389 41 41-45 70 160 5.08 140-170 23.0 130 4.87 84
9 12681 50 46-50 71 195 5.27 170-200 27.2 112 4.72 70
10 10005 43 41-45 68 187 5.23 170-200 28.4 120 4.79 80
# ... with 3,144 more rows, and 11 more variables: chol <int>,
# behpat <fct>, dibpat <fct>, smoke <fct>, ncigs <int>, arcus <int>,
# chd69 <fct>, typchd69 <int>, time169 <int>, t1 <dbl>, uni <dbl>Here, we have 3154 rows (subjects) and 22 columns (variables). Since I used read.csv to import the data, and then converted to a tibble, all variables containing character data will appear as factors.
13.1.1 Structure of wcgs
We can specify the (sometimes terrible) variable names, through the names function, or we can add other elements of the structure, so that we can identify elements of particular interest.
Classes 'tbl_df', 'tbl' and 'data.frame': 3154 obs. of 22 variables:
$ id : int 2343 3656 3526 22057 12927 16029 3894 11389 12681 10005 ...
$ age : int 50 51 59 51 44 47 40 41 50 43 ...
$ agec : Factor w/ 5 levels "35-40","41-45",..: 3 4 5 4 2 3 1 2 3 2 ...
$ height : int 67 73 70 69 71 64 70 70 71 68 ...
$ weight : int 200 192 200 150 160 158 162 160 195 187 ...
$ lnwght : num 5.3 5.26 5.3 5.01 5.08 ...
$ wghtcat : Factor w/ 4 levels "< 140","> 200",..: 4 4 4 3 3 3 3 3 4 4 ...
$ bmi : num 31.3 25.3 28.7 22.1 22.3 ...
$ sbp : int 132 120 158 126 126 116 122 130 112 120 ...
$ lnsbp : num 4.88 4.79 5.06 4.84 4.84 ...
$ dbp : int 90 74 94 80 80 76 78 84 70 80 ...
$ chol : int 249 194 258 173 214 206 190 212 130 233 ...
$ behpat : Factor w/ 4 levels "A1","A2","B3",..: 1 1 1 1 1 1 1 1 1 1 ...
$ dibpat : Factor w/ 2 levels "Type A","Type B": 1 1 1 1 1 1 1 1 1 1 ...
$ smoke : Factor w/ 2 levels "No","Yes": 2 2 1 1 1 2 1 2 1 2 ...
$ ncigs : int 25 25 0 0 0 80 0 25 0 25 ...
$ arcus : int 1 0 1 1 0 0 0 0 1 0 ...
$ chd69 : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 ...
$ typchd69: int 0 0 0 0 0 0 0 0 0 0 ...
$ time169 : int 1367 2991 2960 3069 3081 2114 2929 3010 3104 2861 ...
$ t1 : num -1.63 -4.06 0.64 1.12 2.43 ...
$ uni : num 0.486 0.186 0.728 0.624 0.379 ...13.1.2 Codebook for wcgs
This table was lovingly hand-crafted, and involved a lot of typing. We’ll look for better ways in 432.
| Name | Stored As | Type | Details (units, levels, etc.) |
|---|---|---|---|
id |
integer | (nominal) | ID #, nominal and uninteresting |
age |
integer | quantitative | age, in years - no decimal places |
agec |
factor (5) | (ordinal) | age: 35-40, 41-45, 46-50, 51-55, 56-60 |
height |
integer | quantitative | height, in inches |
weight |
integer | quantitative | weight, in pounds |
lnwght |
number | quantitative | natural logarithm of weight |
wghtcat |
factor (4) | (ordinal) | wt: < 140, 140-170, 170-200, > 200 |
bmi |
number | quantitative | body-mass index: |
| 703 * weight in lb / (height in in)2 | |||
sbp |
integer | quantitative | systolic blood pressure, in mm Hg |
lnsbp |
number | quantitative | natural logarithm of sbp |
dbp |
integer | quantitative | diastolic blood pressure, mm Hg |
chol |
integer | quantitative | total cholesterol, mg/dL |
behpat |
factor (4) | (nominal) | behavioral pattern: A1, A2, B3 or B4 |
dibpat |
factor (2) | (binary) | behavioral pattern: A or B |
smoke |
factor (2) | (binary) | cigarette smoker: Yes or No |
ncigs |
integer | quantitative | number of cigarettes smoked per day |
arcus |
integer | (nominal) | arcus senilis present (1) or absent (0) |
chd69 |
factor (2) | (binary) | CHD event: Yes or No |
typchd69 |
integer | (4 levels) | event: 0 = no CHD, 1 = MI or SD, |
| 2 = silent MI, 3 = angina | |||
time169 |
integer | quantitative | follow-up time in days |
t1 |
number | quantitative | heavy-tailed (random draws) |
uni |
number | quantitative | light-tailed (random draws) |
13.1.3 Quick Summary
id age agec height weight
Min. : 2001 Min. :39.0 35-40: 543 Min. :60.0 Min. : 78
1st Qu.: 3741 1st Qu.:42.0 41-45:1091 1st Qu.:68.0 1st Qu.:155
Median :11406 Median :45.0 46-50: 750 Median :70.0 Median :170
Mean :10478 Mean :46.3 51-55: 528 Mean :69.8 Mean :170
3rd Qu.:13115 3rd Qu.:50.0 56-60: 242 3rd Qu.:72.0 3rd Qu.:182
Max. :22101 Max. :59.0 Max. :78.0 Max. :320
lnwght wghtcat bmi sbp lnsbp
Min. :4.36 < 140 : 232 Min. :11.2 Min. : 98 Min. :4.58
1st Qu.:5.04 > 200 : 213 1st Qu.:23.0 1st Qu.:120 1st Qu.:4.79
Median :5.14 140-170:1538 Median :24.4 Median :126 Median :4.84
Mean :5.13 170-200:1171 Mean :24.5 Mean :129 Mean :4.85
3rd Qu.:5.20 3rd Qu.:25.8 3rd Qu.:136 3rd Qu.:4.91
Max. :5.77 Max. :38.9 Max. :230 Max. :5.44
dbp chol behpat dibpat smoke
Min. : 58 Min. :103 A1: 264 Type A:1589 No :1652
1st Qu.: 76 1st Qu.:197 A2:1325 Type B:1565 Yes:1502
Median : 80 Median :223 B3:1216
Mean : 82 Mean :226 B4: 349
3rd Qu.: 86 3rd Qu.:253
Max. :150 Max. :645
NA's :12
ncigs arcus chd69 typchd69 time169
Min. : 0.0 Min. :0.000 No :2897 Min. :0.000 Min. : 18
1st Qu.: 0.0 1st Qu.:0.000 Yes: 257 1st Qu.:0.000 1st Qu.:2842
Median : 0.0 Median :0.000 Median :0.000 Median :2942
Mean :11.6 Mean :0.299 Mean :0.136 Mean :2684
3rd Qu.:20.0 3rd Qu.:1.000 3rd Qu.:0.000 3rd Qu.:3037
Max. :99.0 Max. :1.000 Max. :3.000 Max. :3430
NA's :2
t1 uni
Min. :-47.4 Min. :0.001
1st Qu.: -1.0 1st Qu.:0.257
Median : 0.0 Median :0.516
Mean : 0.0 Mean :0.505
3rd Qu.: 1.0 3rd Qu.:0.756
Max. : 47.0 Max. :0.999
NA's :39 For a more detailed description, we might consider Hmisc::describe, psych::describe, mosaic::favstats, etc.
13.2 Are the SBPs Normally Distributed?
Consider the question of whether the distribution of the systolic blood pressure results is well-approximated by the Normal.
res <- mosaic::favstats(~ sbp, data = wcgs)
bin_w <- 5 # specify binwidth
ggplot(wcgs, aes(x = sbp)) +
geom_histogram(binwidth = bin_w,
fill = "orchid",
col = "blue") +
theme_bw() +
stat_function(
fun = function(x) dnorm(x, mean = res$mean,
sd = res$sd) *
res$n * bin_w,
col = "navy") +
labs(title = "Systolic BP for `wcgs` subjects",
x = "Systolic BP (mm Hg)", y = "",
caption = "Superimposed Normal model")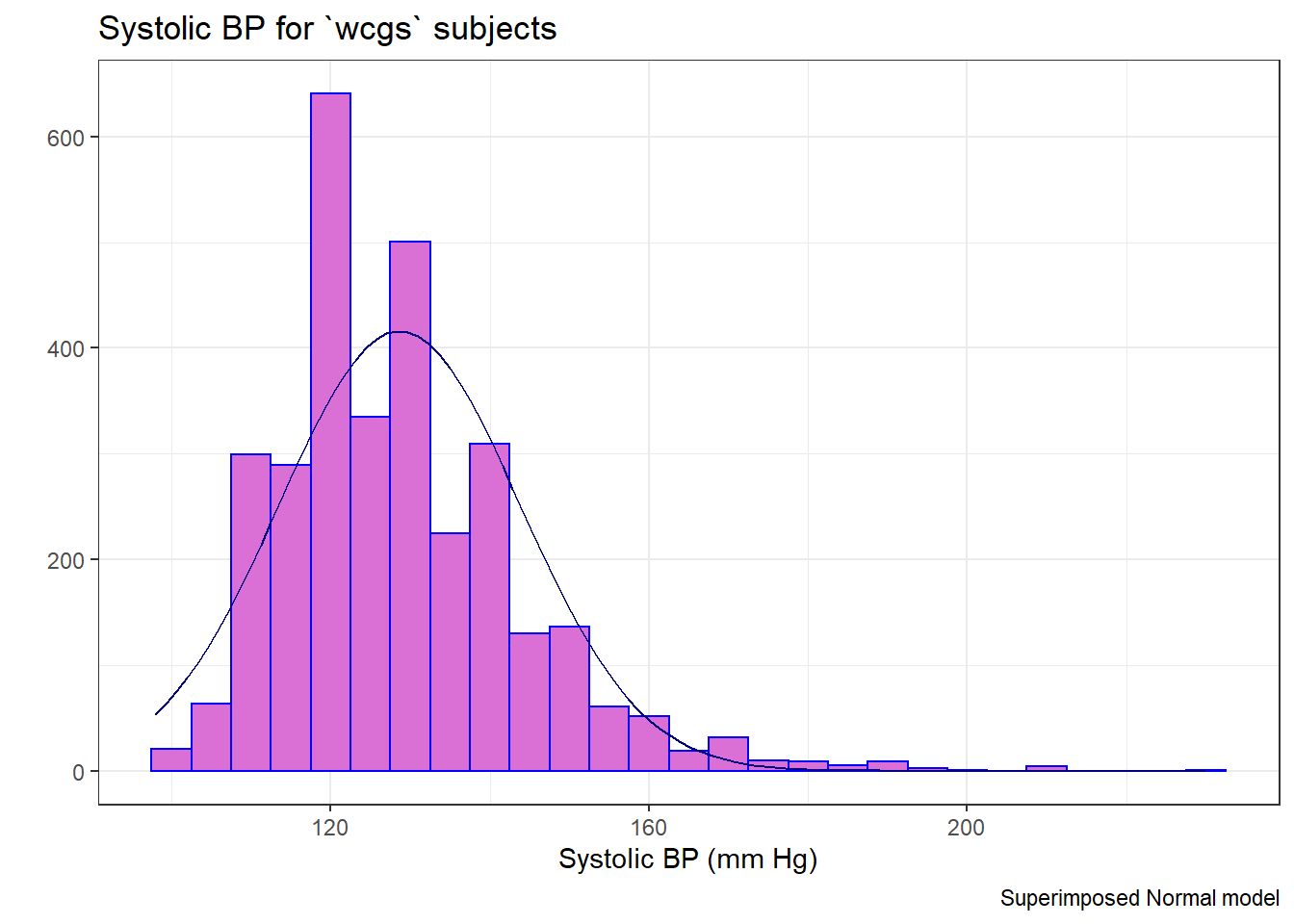
Since the data contain both sbp and lnsbp (its natural logarithm), let’s compare them. Note that in preparing the graph, we’ll need to change the location for the text annotation.
res <- mosaic::favstats(~ lnsbp, data = wcgs)
bin_w <- 0.05 # specify binwidth
ggplot(wcgs, aes(x = lnsbp)) +
geom_histogram(binwidth = bin_w,
fill = "orange",
col = "blue") +
theme_bw() +
stat_function(
fun = function(x) dnorm(x, mean = res$mean,
sd = res$sd) *
res$n * bin_w,
col = "navy") +
labs(title = "ln(Systolic BP) for `wcgs` subjects",
x = "ln(Systolic BP)", y = "",
caption = "Superimposed Normal model")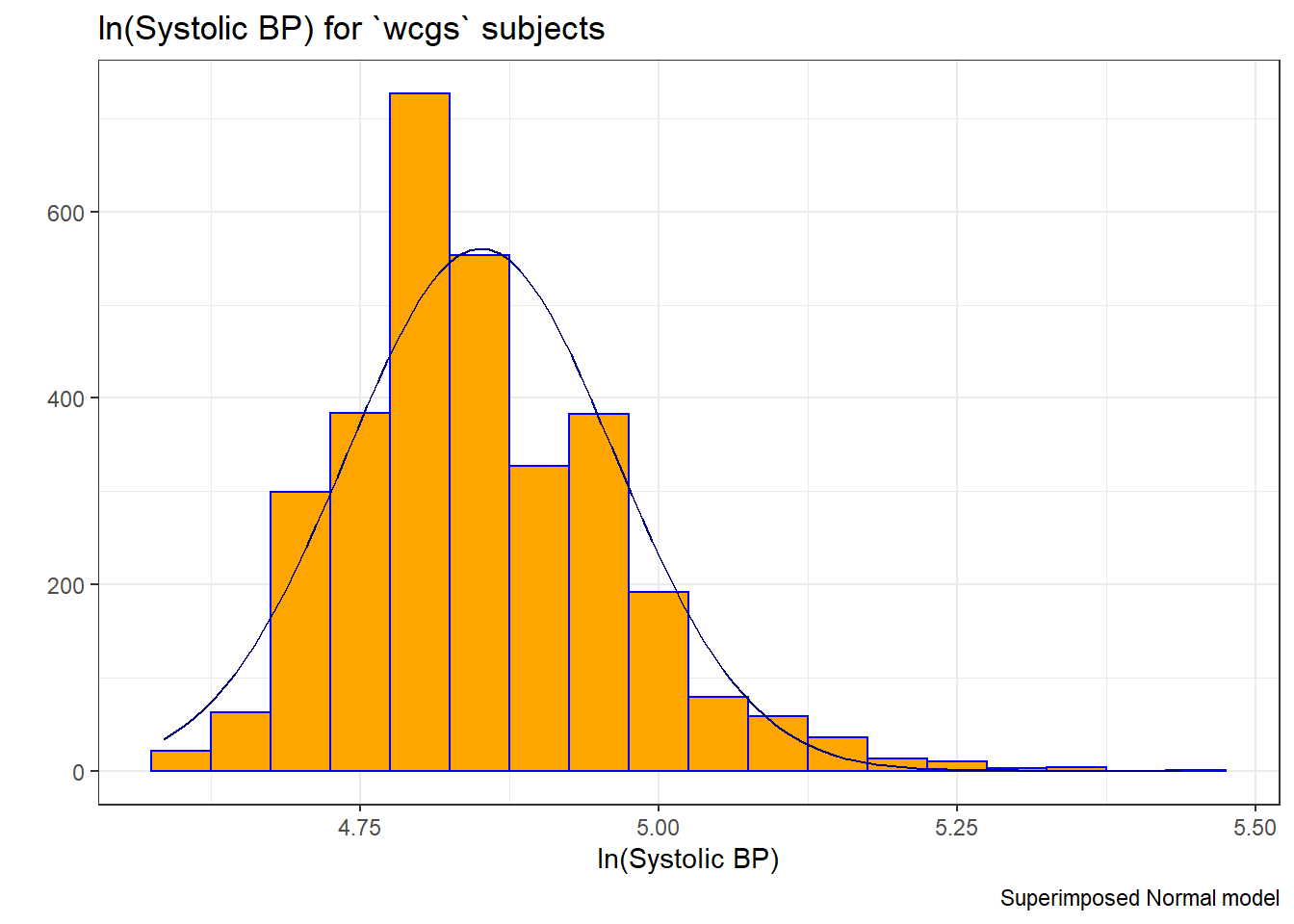
We can also look at Normal Q-Q plots, for instance…
p1 <- ggplot(wcgs, aes(sample = sbp)) +
geom_qq(color = "orchid") +
geom_qq_line(color = "red") +
labs(y = "Ordered SBP", title = "sbp in wcgs")
p2 <- ggplot(wcgs, aes(sample = lnsbp)) +
geom_qq(color = "orange") +
geom_qq_line(color = "red") +
labs(y = "Ordered ln(SBP)", title = "ln(sbp) in wcgs")
## next step requires library(patchwork)
p1 + p2 +
plot_annotation(title = "Normal Q-Q plots of SBP and ln(SBP) in wcgs")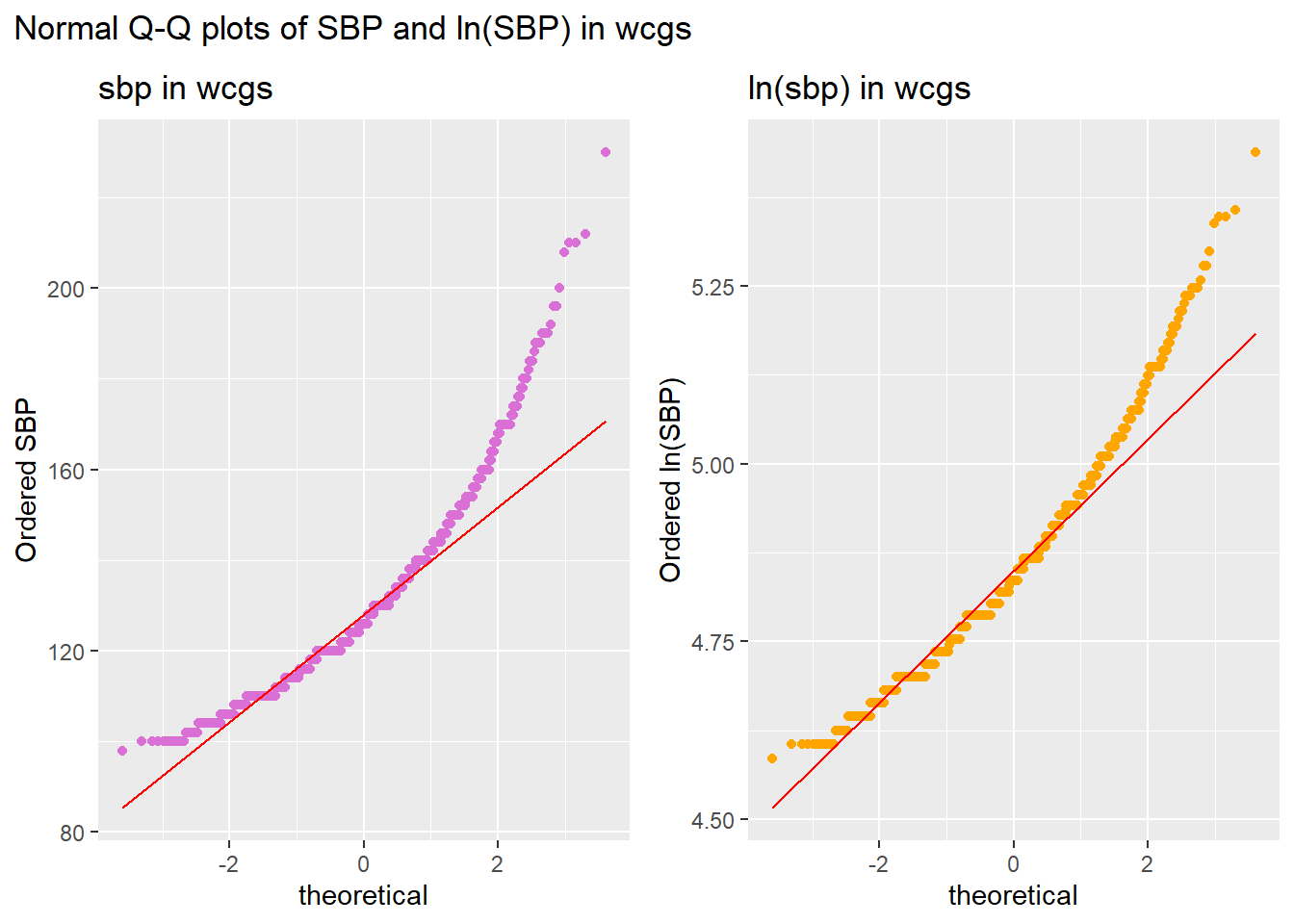
There’s at best a small improvement from sbp to lnsbp in terms of approximation by a Normal distribution.
13.3 Describing Outlying Values with Z Scores
It looks like there’s an outlier (or a series of them) in the SBP data.
ggplot(wcgs, aes(x = "", y = sbp)) +
geom_violin() +
geom_boxplot(width = 0.3, fill = "royalblue",
outlier.color = "royalblue") +
labs(title = "Boxplot with Violin of SBP in `wcgs` data",
y = "Systolic Blood Pressure (mm Hg)",
x = "") +
theme_light() +
coord_flip() 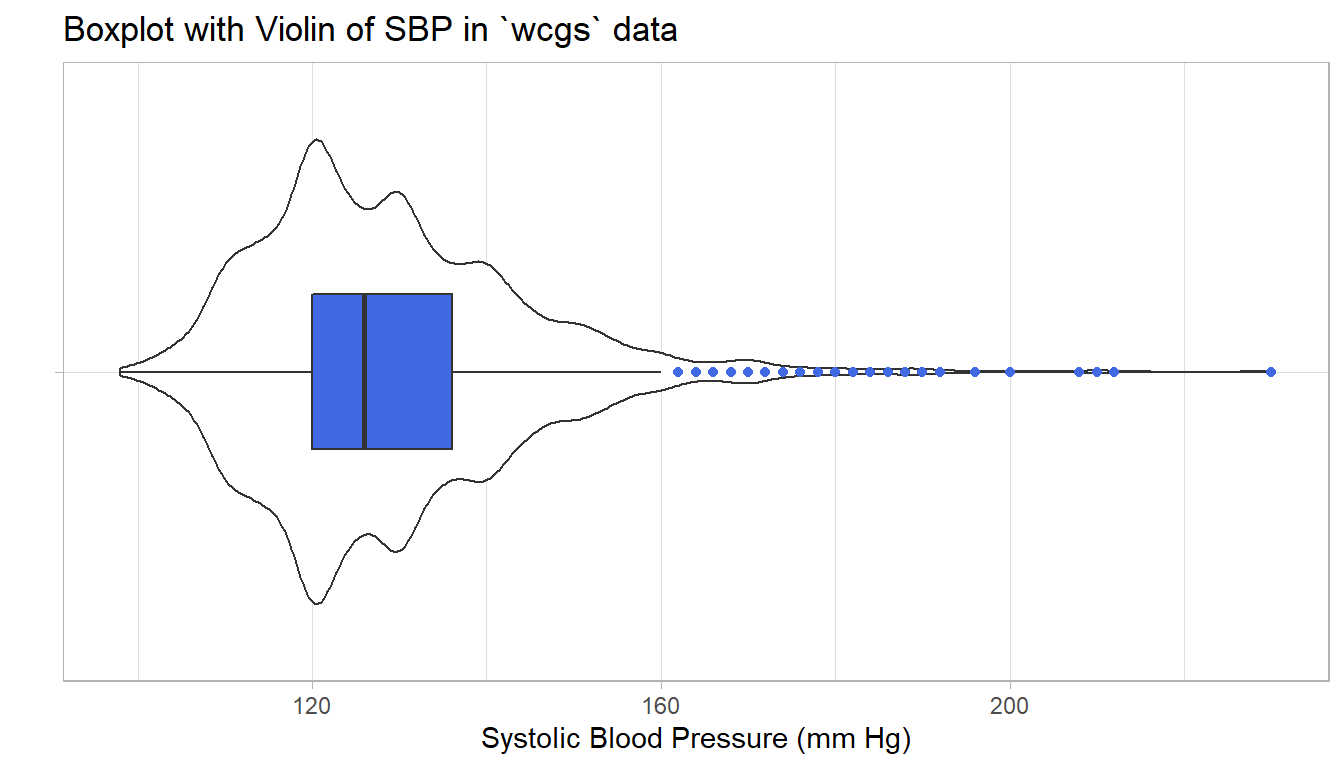
sbp
n missing distinct Info Mean Gmd .05 .10
3154 0 62 0.996 128.6 16.25 110 112
.25 .50 .75 .90 .95
120 126 136 148 156
lowest : 98 100 102 104 106, highest: 200 208 210 212 230The maximum value here is 230, and is clearly the most extreme value in the data set. One way to gauge this is to describe that observation’s Z score, the number of standard deviations away from the mean that the observation falls. Here, the maximum value, 230 is 6.71 standard deviations above the mean, and thus has a Z score of 6.7.
A negative Z score would indicate a point below the mean, while a positive Z score indicates, as we’ve seen, a point above the mean. The minimum systolic blood pressure, 98 is 2.03 standard deviations below the mean, so it has a Z score of -2.
Recall that the Empirical Rule suggests that if a variable follows a Normal distribution, it would have approximately 95% of its observations falling inside a Z score of (-2, 2), and 99.74% falling inside a Z score range of (-3, 3). Do the systolic blood pressures appear Normally distributed?
13.4 Does Weight Category Relate to SBP?
The data are collected into four groups based on the subject’s weight (in pounds).
ggplot(wcgs, aes(x = wghtcat, y = sbp)) +
geom_violin() +
geom_boxplot(aes(fill = wghtcat), width = 0.3, notch = TRUE) +
scale_fill_viridis_d() +
guides(fill = FALSE) +
labs(title = "Boxplot of Systolic BP by Weight Category in WCGS",
x = "Weight Category", y = "Systolic Blood Pressure")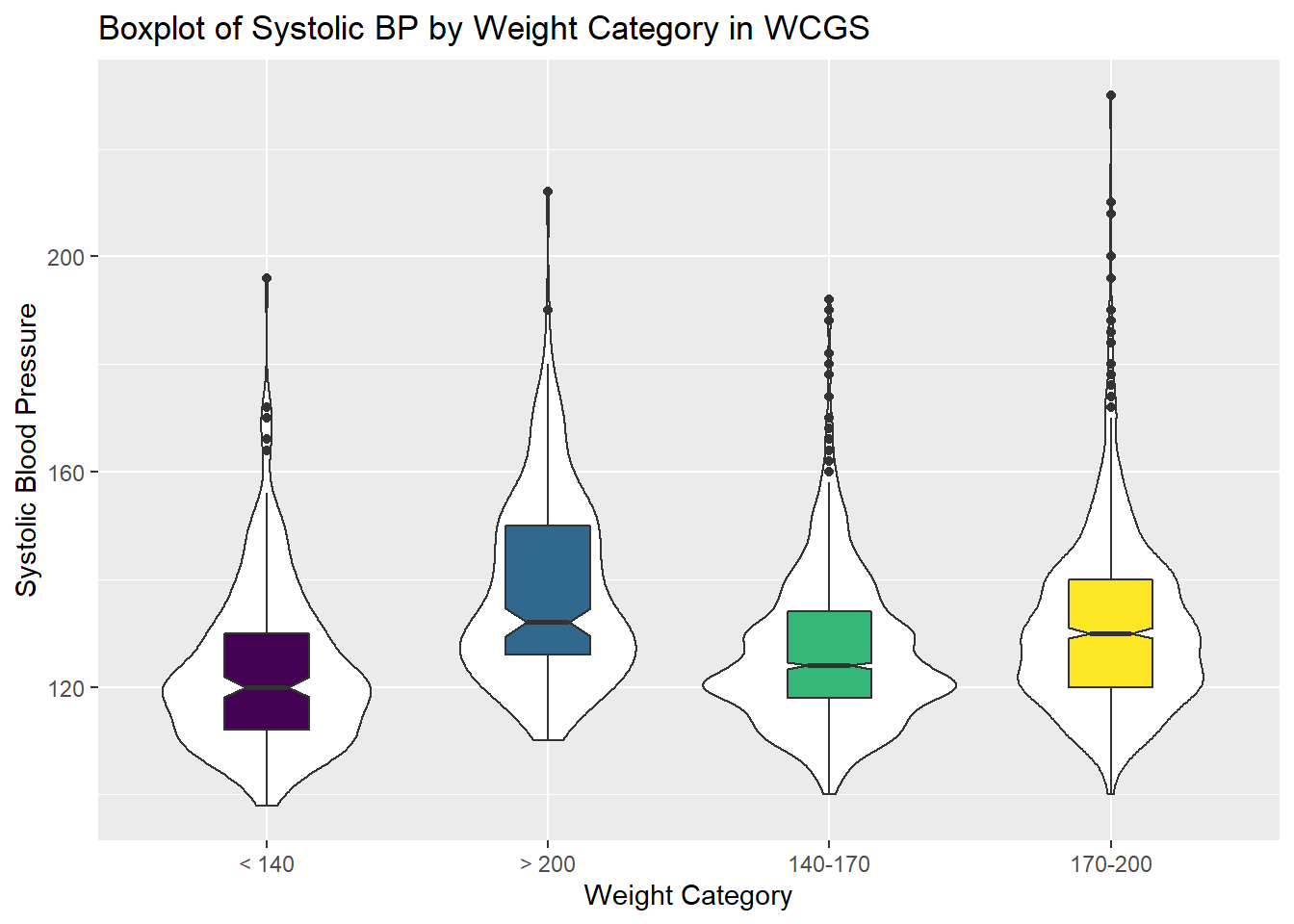
13.5 Re-Leveling a Factor
Well, that’s not so good. We really want those weight categories (the levels) to be ordered more sensibly.
wghtcat n percent
< 140 232 0.0736
> 200 213 0.0675
140-170 1538 0.4876
170-200 1171 0.3713Like all factor variables in R, the categories are specified as levels.
[1] "< 140" "> 200" "140-170" "170-200"We want to change the order of the levels in a new version of this factor variable so they make sense. There are multiple ways to do this, but I prefer the fct_relevel function from the forcats package. Which order is more appropriate?
I’ll add a new variable to the wcgs data called weight_f that relevels the wghtcat data.
wcgs <- wcgs %>%
mutate(weight_f = fct_relevel(wghtcat, "< 140", "140-170", "170-200", "> 200"))
wcgs %>% tabyl(weight_f) weight_f n percent
< 140 232 0.0736
140-170 1538 0.4876
170-200 1171 0.3713
> 200 213 0.0675For more on the forcats package, check out Grolemund and Wickham (2019), especially the Section on Factors.
13.5.1 SBP by Weight Category
ggplot(wcgs, aes(x = weight_f, y = sbp, fill = weight_f)) +
geom_boxplot(notch = TRUE) +
scale_fill_viridis_d() +
guides(fill = FALSE) +
labs(title = "Systolic Blood Pressure by Reordered Weight Category in WCGS",
x = "Weight Category", y = "Systolic Blood Pressure")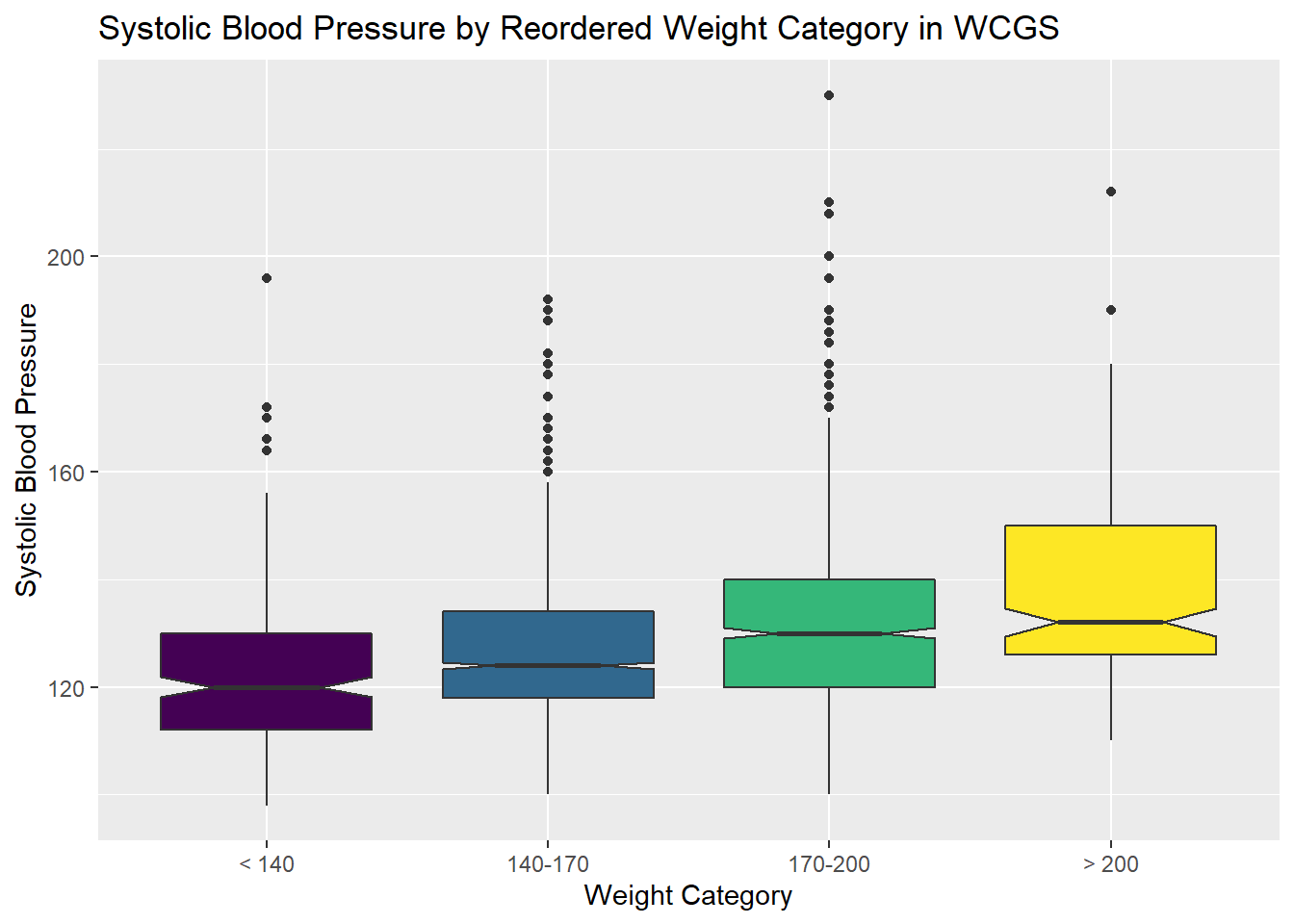
We might see some details well with a ridgeline plot, too.
wcgs %>%
ggplot(aes(x = sbp, y = weight_f, fill = weight_f, height = ..density..)) +
ggridges::geom_density_ridges(scale = 2) +
scale_fill_viridis_d() +
guides(fill = FALSE) +
labs(title = "SBP by Weight Category (wcgs)",
x = "Systolic Blood Pressure",
y = "Weight Category") +
theme_bw()Picking joint bandwidth of 3.74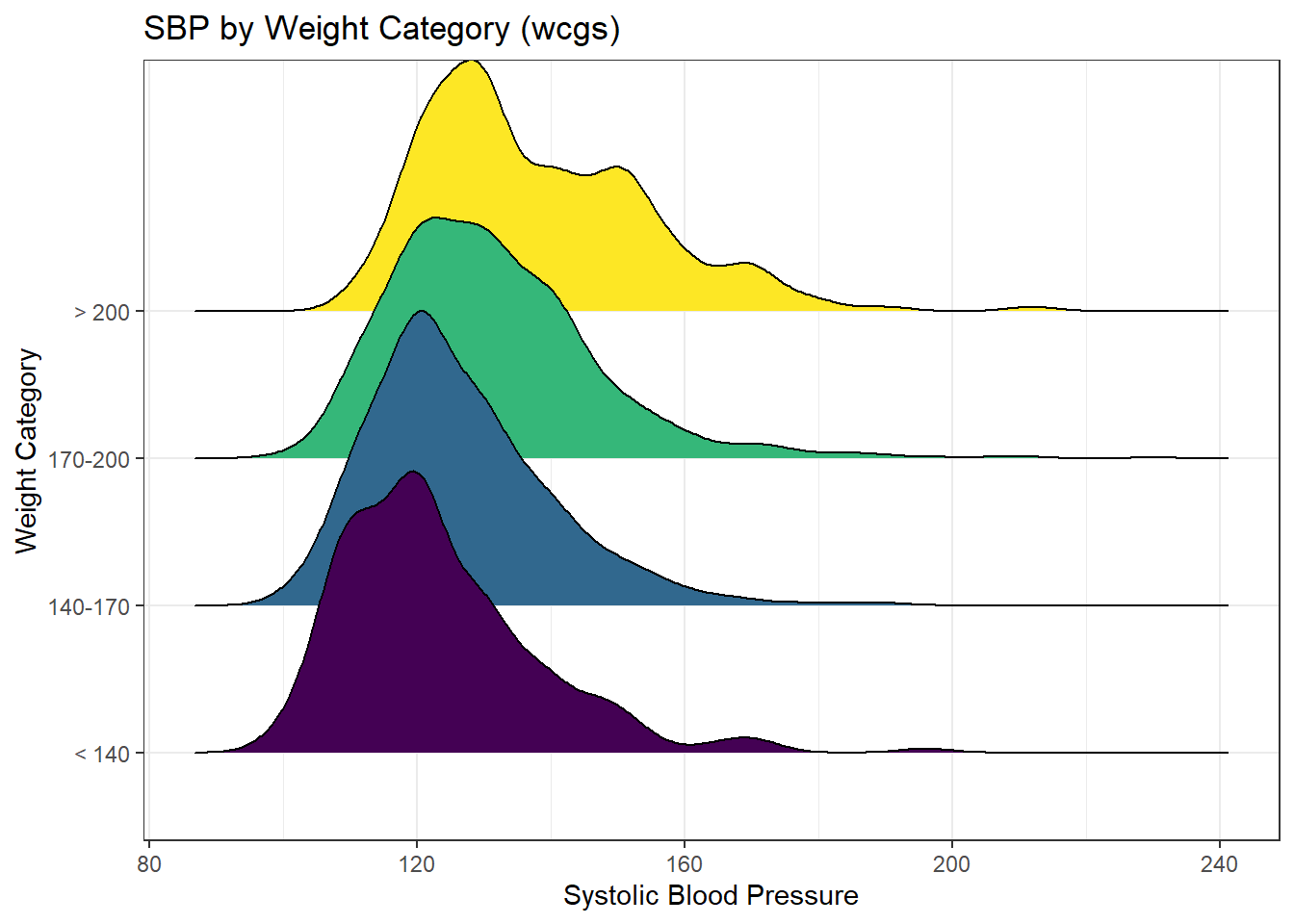
As the plots suggest, patients in the heavier groups generally had higher systolic blood pressures.
weight_f min Q1 median Q3 max mean sd n missing
1 < 140 98 112 120 130 196 123 14.7 232 0
2 140-170 100 118 124 134 192 126 13.7 1538 0
3 170-200 100 120 130 140 230 131 15.6 1171 0
4 > 200 110 126 132 150 212 138 16.8 213 013.6 Are Weight and SBP Linked?
Let’s build a scatter plot of SBP (Outcome) by Weight (Predictor), rather than breaking down into categories.
ggplot(wcgs, aes(x = weight, y = sbp)) +
geom_point(size=3, shape=1, color="forestgreen") + ## default size = 2
stat_smooth(method=lm, color="red") + ## add se=FALSE to hide conf. interval
stat_smooth(method=loess, se=FALSE, color="blue") +
ggtitle("SBP vs. Weight in 3,154 WCGS Subjects") +
theme_bw()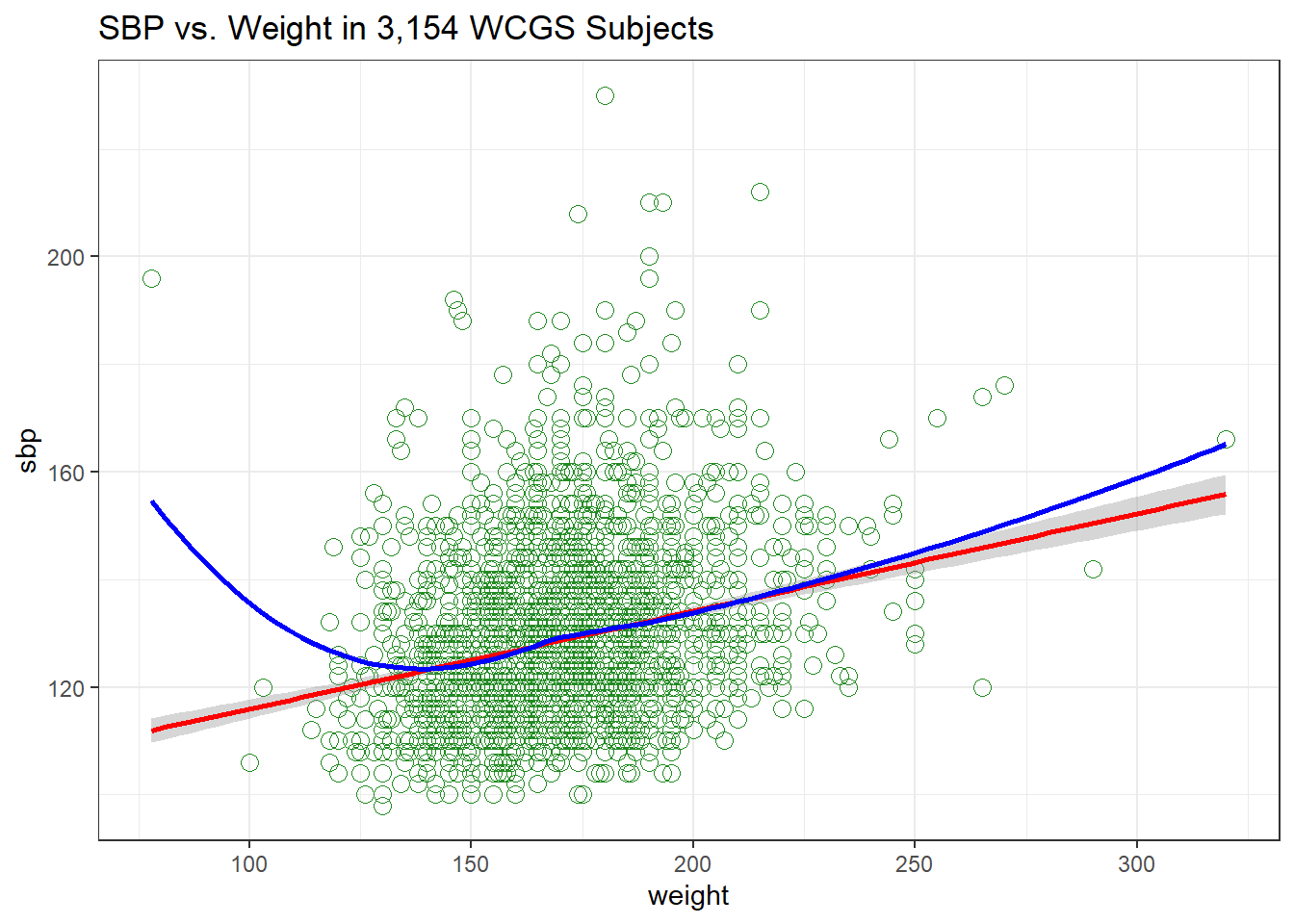
- The mass of the data is hidden from us - showing 3154 points in one plot can produce little more than a blur where there are lots of points on top of each other.
- Here the least squares regression line (in red), and loess scatterplot smoother, (in blue) can help.
The relationship between systolic blood pressure and weight appears to be very close to linear, but of course there is considerable scatter around that generally linear relationship. It turns out that the Pearson correlation of these two variables is 0.253.
13.7 SBP and Weight by Arcus Senilis groups?
An issue of interest to us will be to assess whether the SBP-Weight relationship we see above is similar among subjects who have arcus senilis and those who do not.
Arcus senilis is an old age syndrome where there is a white, grey, or blue opaque ring in the corneal margin (peripheral corneal opacity), or white ring in front of the periphery of the iris. It is present at birth but then fades; however, it is quite commonly present in the elderly. It can also appear earlier in life as a result of hypercholesterolemia.
Wikipedia article on Arcus Senilis, retrieved 2017-08-15
Let’s start with a quick look at the arcus data.
arcus n percent valid_percent
0 2211 0.701015 0.701
1 941 0.298351 0.299
NA 2 0.000634 NAWe have 2 missing values, so we probably want to do something about that before plotting the data, and we may also want to create a factor variable with more meaningful labels than 1 (which means yes, arcus senilis is present) and 0 (which means no, it isn’t.)
wcgs <- wcgs %>%
mutate(arcus_f = fct_recode(factor(arcus),
"Arcus senilis" = "1",
"No arcus senilis" = "0"),
arcus_f = fct_relevel(arcus_f, "Arcus senilis"))
wcgs %>% tabyl(arcus_f, arcus) arcus_f 0 1 NA_
Arcus senilis 0 941 0
No arcus senilis 2211 0 0
<NA> 0 0 2Let’s build a version of the wcgs data that eliminates all missing data in the variables of immediate interest, and then plot the SBP-weight relationship in groups of patients with and without arcus senilis.
wcgs %>%
filter(complete.cases(arcus_f, sbp, weight)) %>%
ggplot(aes(x = weight, y = sbp, group = arcus_f)) +
geom_point(shape = 1) +
stat_smooth(method=lm, color="red") +
stat_smooth(method=loess, se=FALSE, color="blue") +
labs(title = "SBP vs. Weight by Arcus Senilis status",
caption = "3,152 Western Collaborative Group Study subjects with known arcus senilis status") +
facet_wrap(~ arcus_f) +
theme_bw()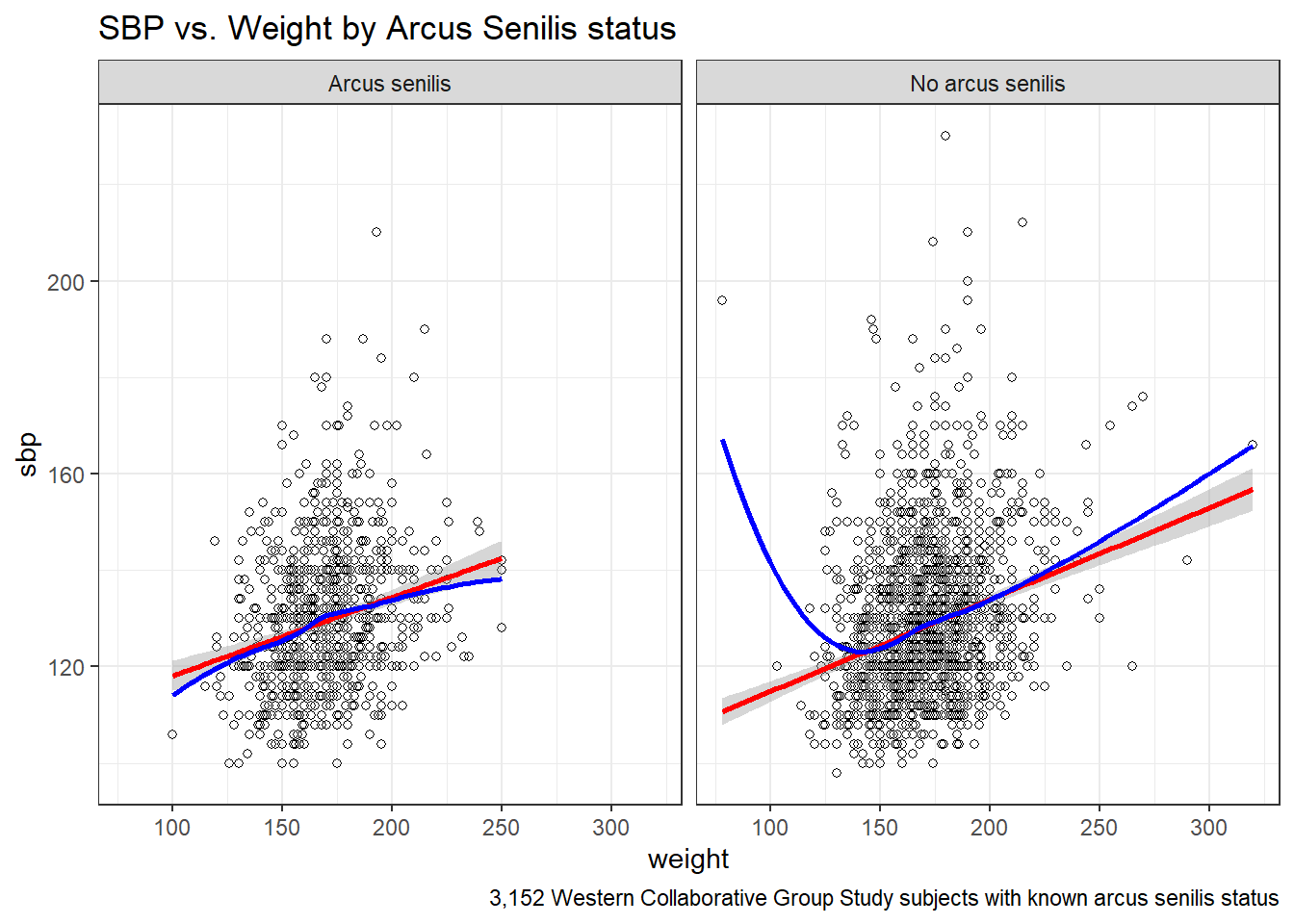
13.8 Linear Model for SBP-Weight Relationship: subjects without Arcus Senilis
Call:
lm(formula = sbp ~ weight, data = filter(wcgs, arcus == 0))
Residuals:
Min 1Q Median 3Q Max
-29.01 -10.25 -2.45 7.55 99.85
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 95.9219 2.5552 37.5 <2e-16 ***
weight 0.1902 0.0149 12.8 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 14.8 on 2209 degrees of freedom
Multiple R-squared: 0.0687, Adjusted R-squared: 0.0683
F-statistic: 163 on 1 and 2209 DF, p-value: <2e-16The linear model for the 2211 patients without Arcus Senilis has R2 = 6.87%.
- The regression equation is 95.92 - 0.19 weight, for those patients without Arcus Senilis.
13.9 Linear Model for SBP-Weight Relationship: subjects with Arcus Senilis
Call:
lm(formula = sbp ~ weight, data = filter(wcgs, arcus == 1))
Residuals:
Min 1Q Median 3Q Max
-30.34 -9.64 -1.96 7.97 76.74
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 101.879 3.756 27.13 < 2e-16 ***
weight 0.163 0.022 7.39 3.3e-13 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 14.2 on 939 degrees of freedom
Multiple R-squared: 0.0549, Adjusted R-squared: 0.0539
F-statistic: 54.6 on 1 and 939 DF, p-value: 3.29e-13The linear model for the 941 patients with Arcus Senilis has R2 = 5.49%.
- The regression equation is 101.88 - 0.163 weight, for those patients with Arcus Senilis.
13.10 Including Arcus Status in the model
Call:
lm(formula = sbp ~ weight * arcus, data = filter(wcgs, !is.na(arcus)))
Residuals:
Min 1Q Median 3Q Max
-30.34 -10.15 -2.35 7.67 99.85
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 95.9219 2.5244 38.00 <2e-16 ***
weight 0.1902 0.0147 12.92 <2e-16 ***
arcus 5.9566 4.6197 1.29 0.20
weight:arcus -0.0276 0.0270 -1.02 0.31
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 14.6 on 3148 degrees of freedom
Multiple R-squared: 0.066, Adjusted R-squared: 0.0651
F-statistic: 74.1 on 3 and 3148 DF, p-value: <2e-16The actual regression equation in this setting includes both weight, and an indicator variable (1 = yes, 0 = no) for arcus senilis status, and the product of weight and that 1/0 indicator.
- Note the use of the product term
weight*arcusin the setup of the model to allow both the slope of weight and the intercept term in the model to change depending on arcus senilis status.- For a patient who has arcus, the regression equation is SBP = 95.92 + 0.19 weight + 5.96 (1) - 0.028 weight (1) = 101.88 + 0.162 weight.
- For a patient without arcus senilis, the regression equation is SBP = 95.92 + 0.19 weight + 5.96 (0) - 0.028 weight (0) = 95.92 + 0.19 weight.
The linear model including the interaction of weight and arcus to predict sbp for the 3152 patients with known Arcus Senilis status has R2 = 6.6%.
13.11 Predictions from these Linear Models
What is our predicted SBP for a subject weighing 175 pounds?
How does that change if our subject weighs 200 pounds?
Recall that
- Without Arcus Senilis, linear model for SBP = 95.9 + 0.19 x weight
- With Arcus Senilis, linear model for SBP = 101.9 + 0.16 x weight
So the predictions for a 175 pound subject are:
95.9 + 0.19 x 175 = 129 mm Hg without Arcus Senilis, and
101.9 + 0.16 x 175 = 130 mm Hg with Arcus Senilis.
And thus, the predictions for a 200 pound subject are:
95.9 + 0.19 x 200 = 134 mm Hg without Arcus Senilis, and
101.9 + 0.16 x 200 = 134.4 mm Hg with Arcus Senilis.
13.12 Scatterplots with Facets Across a Categorical Variable
We can use facets in ggplot2 to show scatterplots across the levels of a categorical variable, like behpat.
ggplot(wcgs, aes(x = weight, y = sbp, col = behpat)) +
geom_point() +
facet_wrap(~ behpat) +
geom_smooth(method = "lm", se = FALSE, col = "black") +
guides(color = FALSE) +
theme(strip.text = element_text(face="bold", size=rel(1.25), color="white"),
strip.background = element_rect(fill="royalblue")) +
labs(title = "Scatterplots of SBP vs. Weight within Behavior Pattern")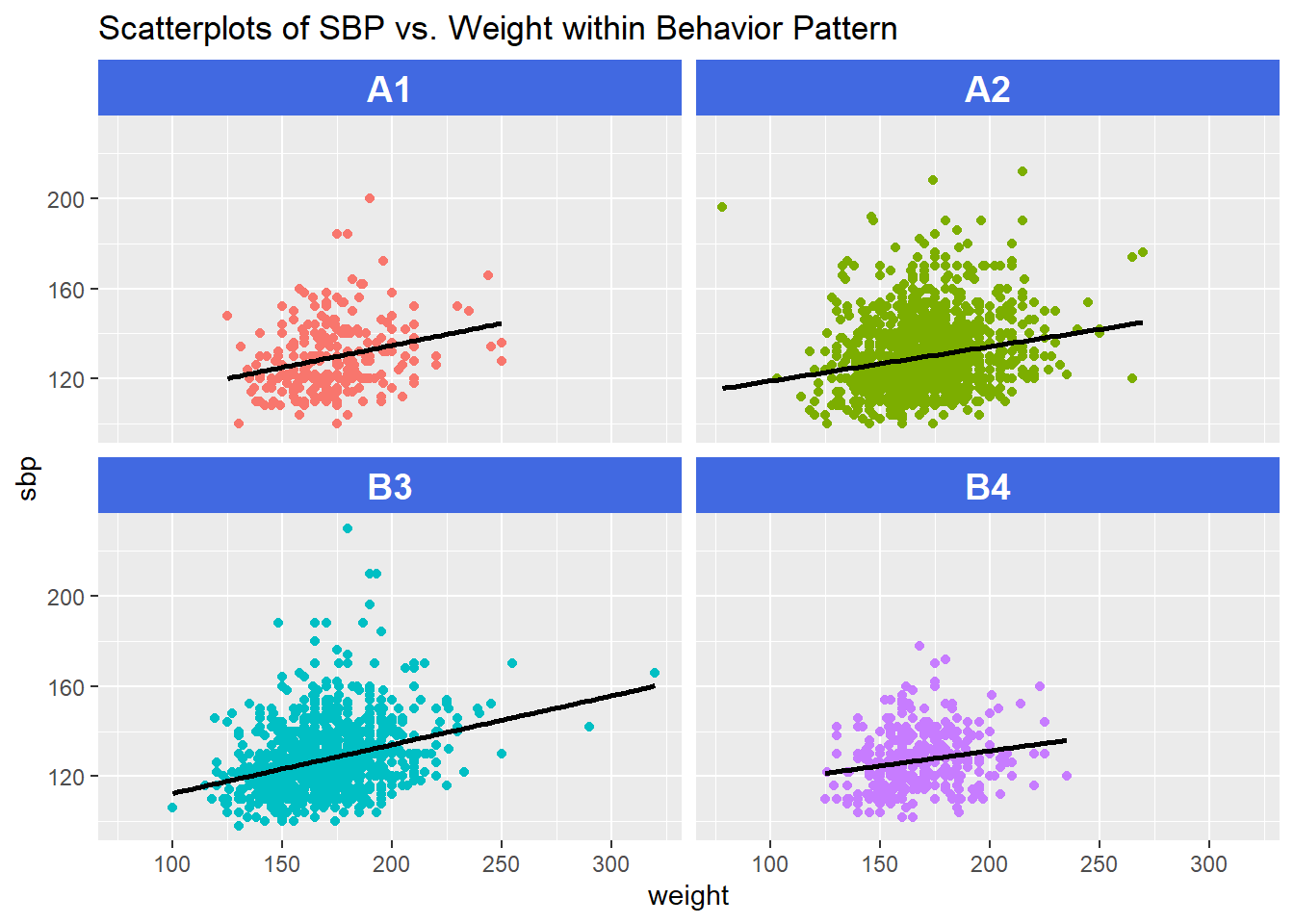
13.13 Scatterplot and Correlation Matrices
A scatterplot matrix can be very helpful in understanding relationships between multiple variables simultaneously. There are several ways to build such a thing, including the pairs function…
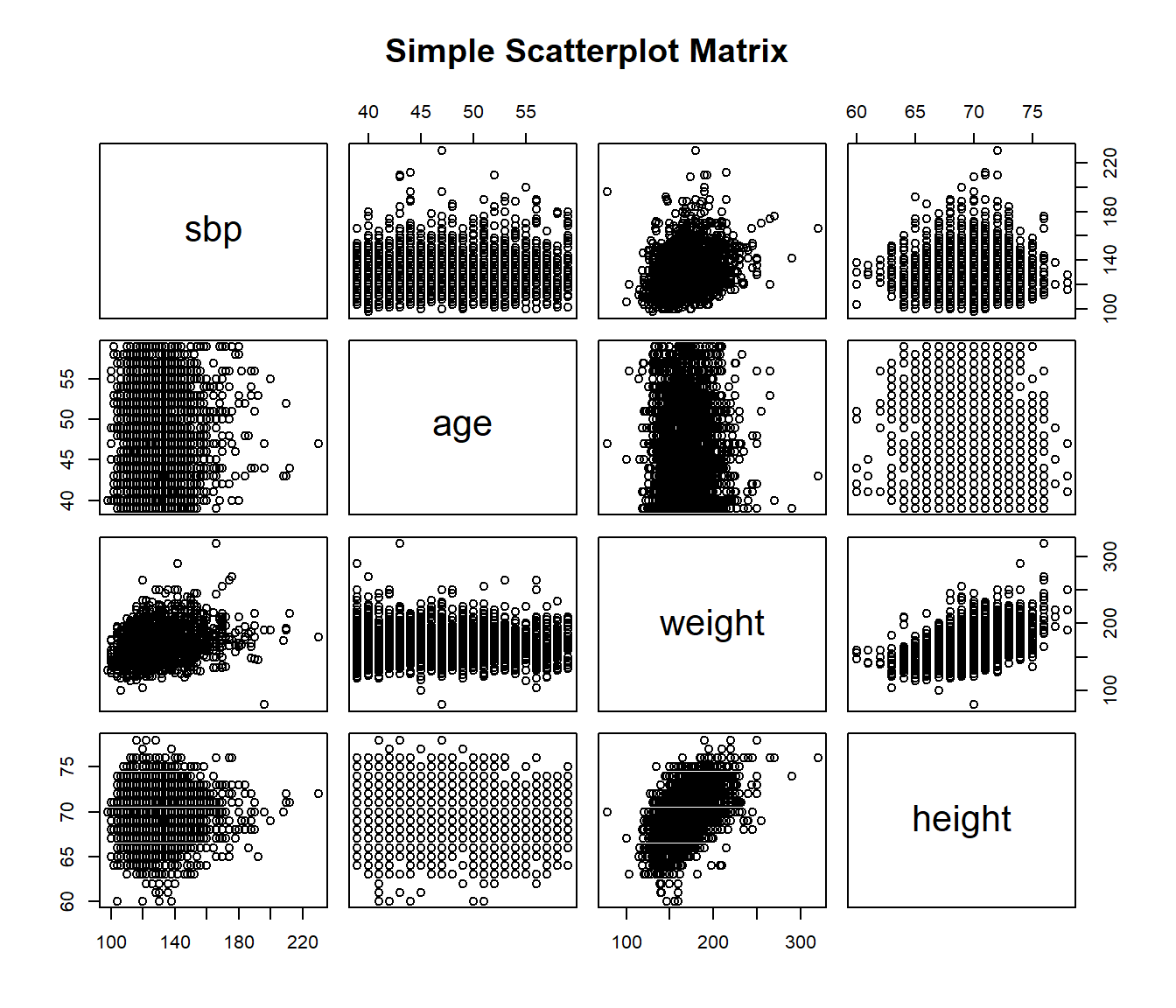
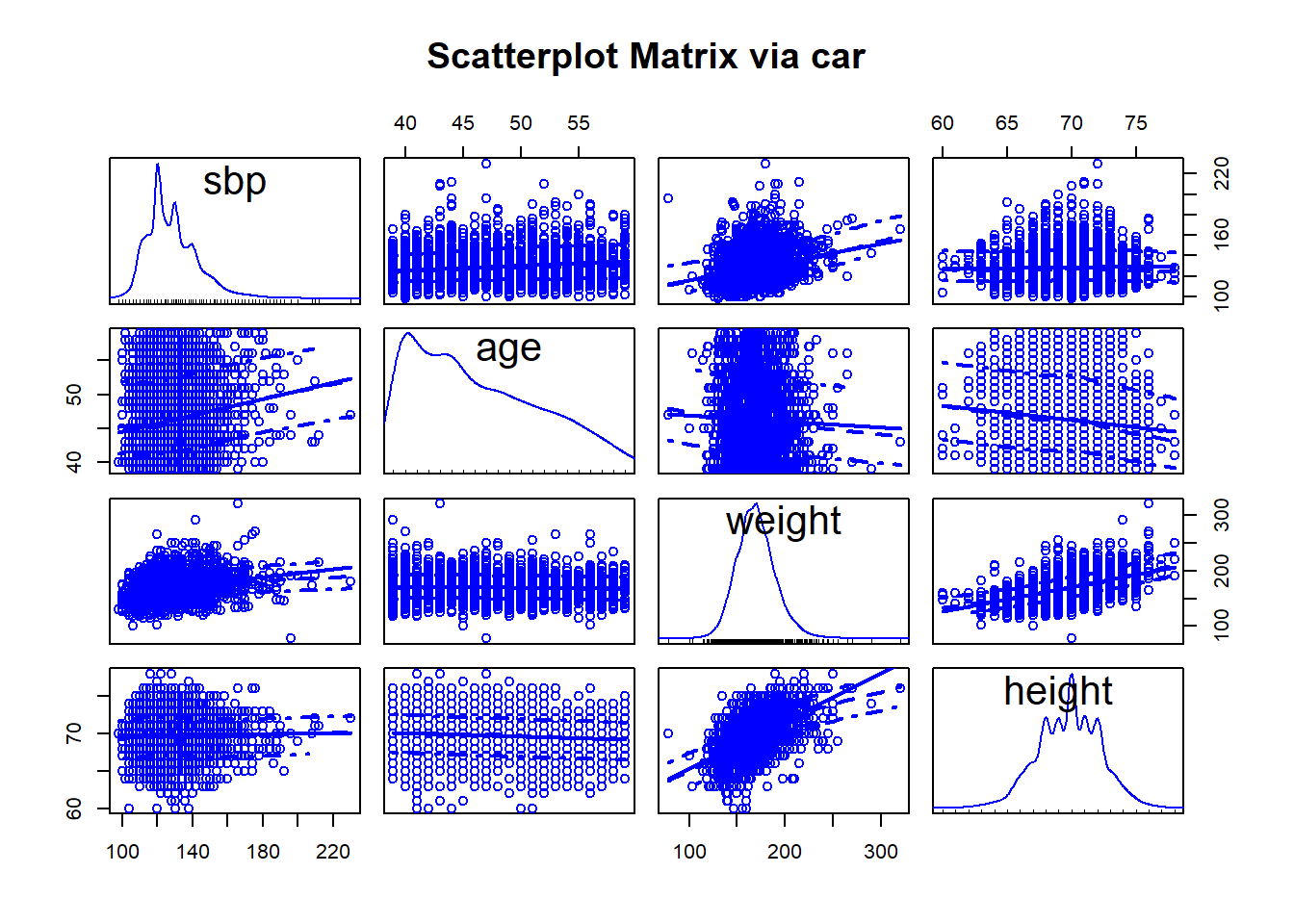
13.13.1 Using the car package
Or, we can use the scatterplotMatrix function from the car package, which adds some detail and fitting to the plots, and places density estimates (with rug plots) on the diagonals.
13.13.2 Displaying a Correlation Matrix
wcgs %>%
dplyr::select(sbp, age, weight, height) %>%
cor() %>% # obtain correlation coefficients for this subgroup
signif(., 3) # round them off to three significant figures before printing sbp age weight height
sbp 1.0000 0.1660 0.2530 0.0184
age 0.1660 1.0000 -0.0344 -0.0954
weight 0.2530 -0.0344 1.0000 0.5330
height 0.0184 -0.0954 0.5330 1.000013.13.3 Using the GGally package
The ggplot2 system doesn’t have a built-in scatterplot system. There are some nice add-ins in the world, though. One option I sort of like is in the GGally package, which can produce both correlation matrices and scatterplot matrices.
The ggpairs function provides a density plot on each diagonal, Pearson correlations on the upper right and scatterplots on the lower left of the matrix.
GGally::ggpairs(wcgs %>% select(sbp, age, weight, height),
title = "Scatterplot Matrix via ggpairs")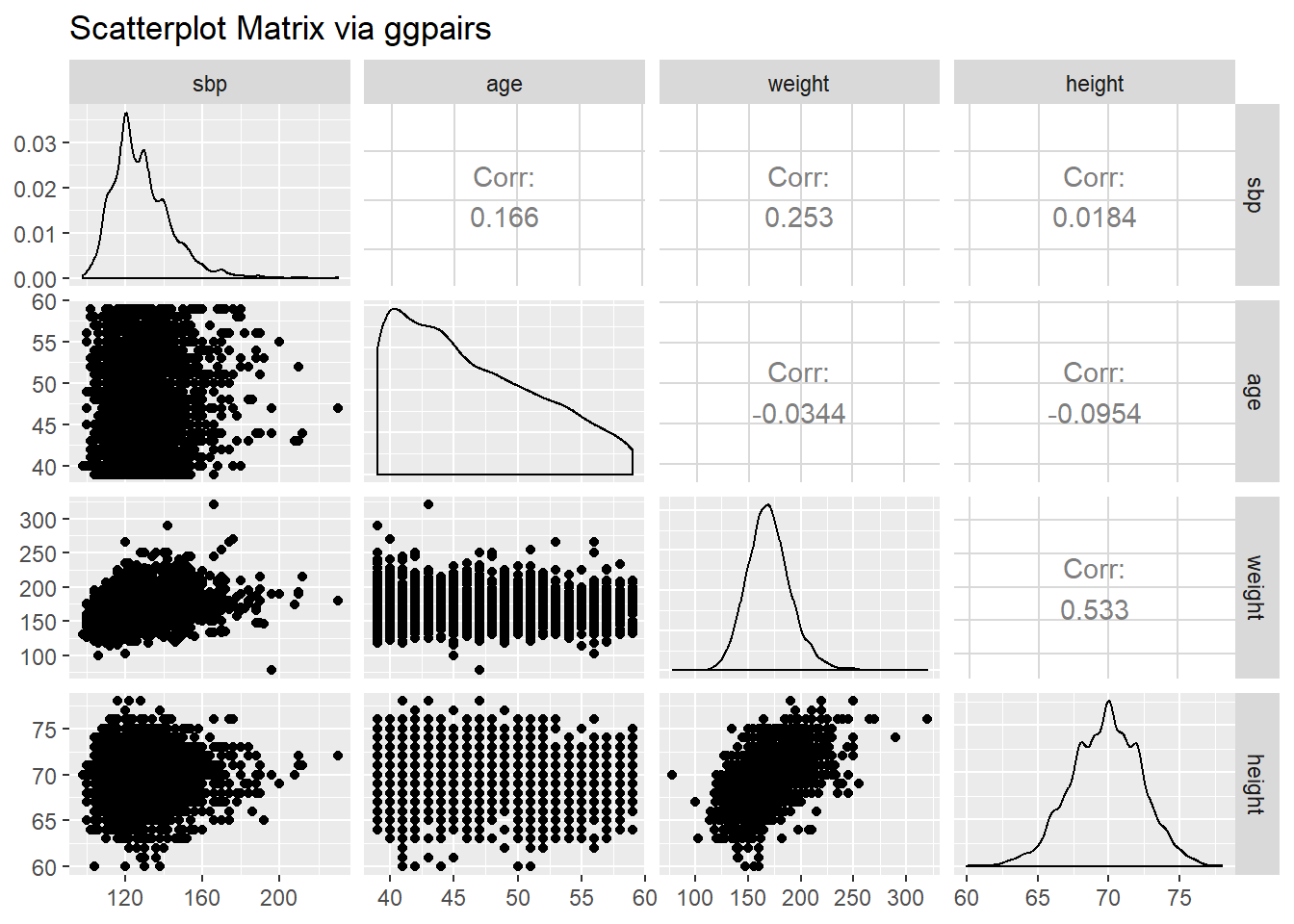
References
Grolemund, Garrett, and Hadley Wickham. 2019. R for Data Science. O’Reilly. http://r4ds.had.co.nz/.
Vittinghoff, Eric, David V. Glidden, Stephen C. Shiboski, and Charles E. McCulloch. 2012. Regression Methods in Biostatistics: Linear, Logistic, Survival, and Repeated Measures Models. Second. Springer-Verlag, Inc. http://www.biostat.ucsf.edu/vgsm/.
For more on the WCGS, you might look at http://www.epi.umn.edu/cvdepi/study-synopsis/western-collaborative-group-study/↩