Chapter 5 Analysis of Variance with SMART

In this chapter, we’ll work with the smart_cle1_sh data file again.

The variables we’ll look at in this chapter are as follows.

Variable Description
SEQNO respondent identification number (all begin with 2016)
bmi Body mass index, in kg/m2
female Sex, 1 = female, 0 = male
smoke100 Have you smoked at least 100 cigarettes in your life? (1 = yes, 0 = no)
activity Physical activity (Highly Active, Active, Insufficiently Active, Inactive)
drinks_wk On average, how many drinks of alcohol do you consume in a week?
physhealth Now thinking about your physical health, which includes physical illness and injury, for how many days during the past 30 days was your physical health not good?

5.1 A One-Factor Analysis of Variance

We’ll be predicting body mass index, at first using a single factor as a predictor: the activity level.

5.1.1 Can activity be used to predict bmi?

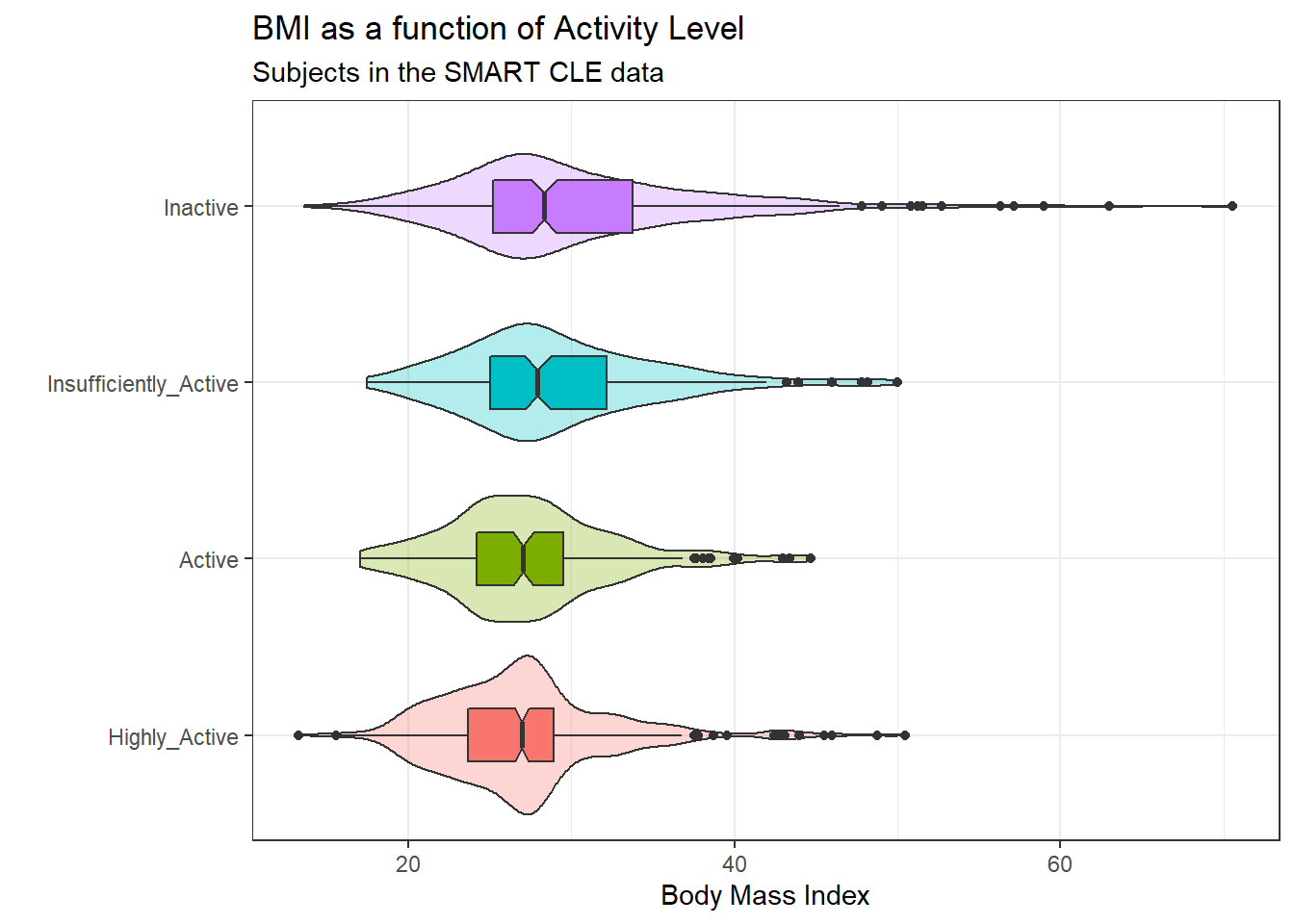
Here’s a numerical summary of the distributions of bmi within each activity group.

               activity   min      Q1   median     Q3   max     mean       sd
1         Highly_Active 13.30 23.6525 26.99000 28.930 50.46 27.02866 5.223417
2                Active 17.07 24.2400 27.06952 29.520 44.67 27.36287 5.150122
3 Insufficiently_Active 17.49 25.0500 27.94014 32.180 49.98 29.04769 6.050899
4              Inactive 13.64 25.2150 28.34000 33.775 70.56 30.16344 7.831596
    n missing
1 428       0
2 173       0
3 201       0
4 331       0

5.1.2 Should we transform bmi?

The analysis of variance is something of a misnomer. What we’re doing is using the variance to say something about population means. In light of the apparent right skew of the bmi results in each activity group, might it be a better choice to use a logarithmic transformation? We’ll use the natural logarithm here, which in R, is symbolized by log.

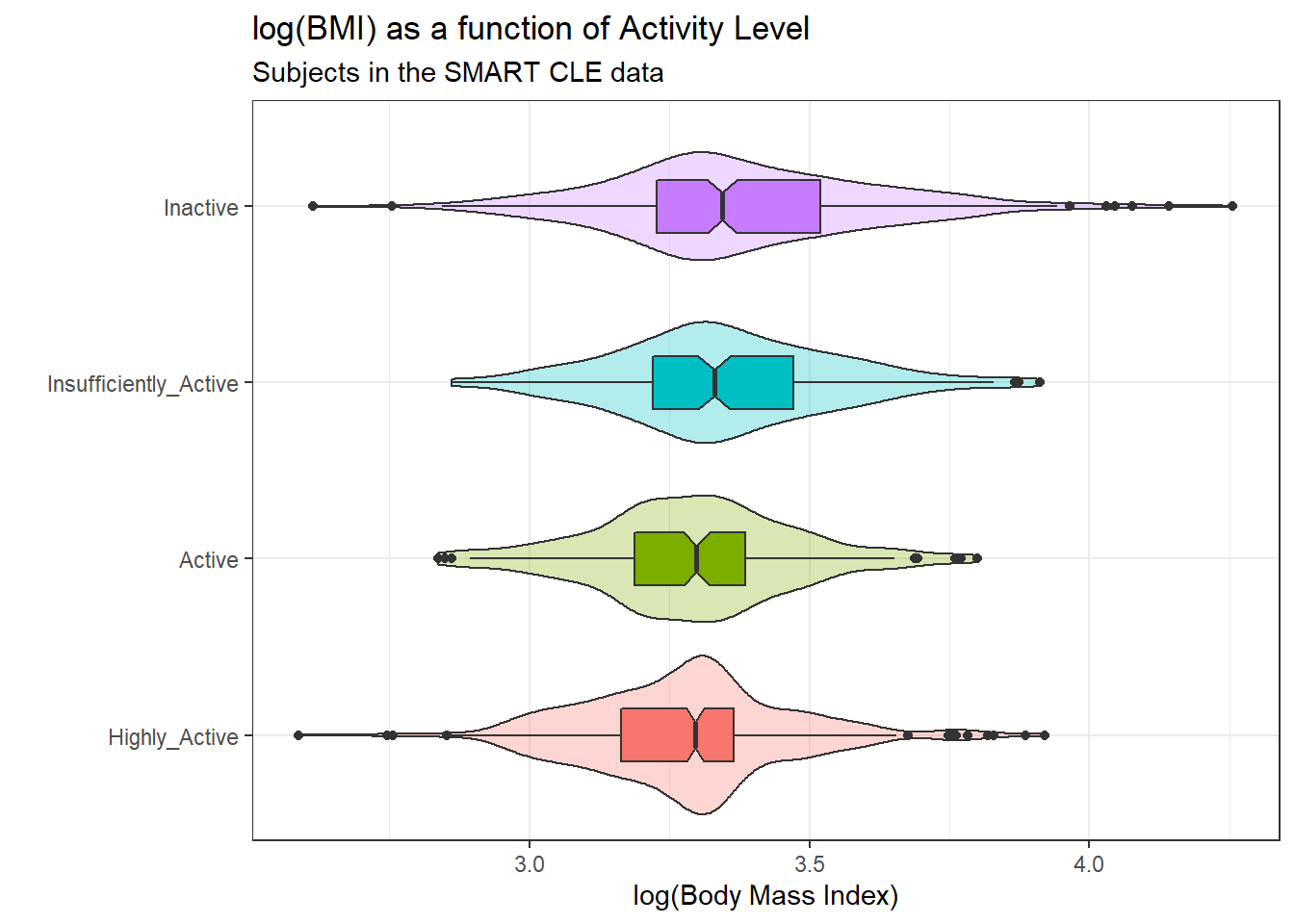
The logarithmic transformation yields distributions that look much more symmetric in each activity group, so we’ll proceed to build our regression model predicting log(bmi) using activity. Here’s the numerical summary of these logged results:

               activity      min       Q1   median       Q3      max     mean
1         Highly_Active 2.587764 3.163469 3.295466 3.364879 3.921181 3.279451
2                Active 2.837323 3.188004 3.298408 3.385068 3.799302 3.292095
3 Insufficiently_Active 2.861629 3.220874 3.330064 3.471345 3.911623 3.348544
4              Inactive 2.613007 3.227439 3.344274 3.519721 4.256463 3.376603
         sd   n missing
1 0.1852463 428       0
2 0.1849678 173       0
3 0.2006914 201       0
4 0.2410612 331       0

5.1.3 Building the ANOVA model


Call:
lm(formula = log(bmi) ~ activity)

Coefficients:
                  (Intercept)                 activityActive  
                      3.27945                        0.01264  
activityInsufficiently_Active               activityInactive  
                      0.06909                        0.09715

The activity data is categorical and there are four levels. The model equation is:

log(bmi) = 3.279 + 0.013 (activity = Active)
                 + 0.069 (activity = Insufficiently Active)
                 + 0.097 (activity = Inactive)

where, for example, (activity = Active) is 1 if activity is Active, and 0 otherwise. The fourth level (Highly Active) is not shown here and is used as a baseline. Thus the model above can be interpreted as follows.

activity Predicted log(bmi) Predicted bmi
Highly Active 3.279 exp(3.279) = 26.55
Active 3.279 + 0.013 = 3.292 exp(3.292) = 26.90
Insufficiently Active 3.279 + 0.069 = 3.348 exp(3.348) = 28.45
Inactive 3.279 + 0.097 = 3.376 exp(3.376) = 29.25

Those predicted log(bmi) values should look familiar. They are just the means of log(bmi) in each group, but I’m sure you’ll also notice that the predicted bmi values are not exact matches for the observed means of bmi.

# A tibble: 4 x 3
  activity              `mean(log(bmi))` `mean(bmi)`
  <fct>                            <dbl>       <dbl>
1 Highly_Active                     3.28        27.0
2 Active                            3.29        27.4
3 Insufficiently_Active             3.35        29.0
4 Inactive                          3.38        30.2

5.1.4 The ANOVA table

Now, let’s press on to look at the ANOVA results for this model.

Analysis of Variance Table

Response: log(bmi)
            Df Sum Sq Mean Sq F value    Pr(>F)    
activity     3  2.058 0.68603  16.214 2.536e-10 ***
Residuals 1129 47.770 0.04231                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  • The total variation in log(bmi), our outcome, is captured by the sums of squares here. SS(Total) = 2.058 + 47.770 = 49.828
  • Here, the activity variable (with 4 levels, so 4-1 = 3 degrees of freedom) accounts for 4.13% (2.058 / 49.828) of the variation in log(bmi). Another way of saying this is that the model \(R^2\) or \(\eta^2\) is 0.0413.
  • The variation accounted for by the activity categories meets the standard for a statistically detectable result, according to the ANOVA F test, although that’s not really important.
  • The square root of the Mean Square(Residuals) is the residual standard error, \(\sigma\), we’ve seen in the past. MS(Residual) estimates the variance (0.0423), so the residual standard error is \(\sqrt{0.0423} \approx 0.206\).

5.1.5 The Model Coefficients

To address the question of effect size for the various levels of activity on log(bmi), we could look directly at the regression model coefficients. For that, we might look at the model summary.


Call:
lm(formula = log(bmi) ~ activity)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.76360 -0.12528 -0.00306  0.11035  0.87986 

Coefficients:
                              Estimate Std. Error t value Pr(>|t|)    
(Intercept)                   3.279451   0.009943 329.833  < 2e-16 ***
activityActive                0.012644   0.018532   0.682    0.495    
activityInsufficiently_Active 0.069093   0.017589   3.928 9.08e-05 ***
activityInactive              0.097153   0.015056   6.453 1.63e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2057 on 1129 degrees of freedom
Multiple R-squared:  0.0413,    Adjusted R-squared:  0.03876 
F-statistic: 16.21 on 3 and 1129 DF,  p-value: 2.536e-10

If we want to see the confidence intervals around these estimates, we could use

                                    2.5 %     97.5 %
(Intercept)                    3.25994254 3.29895925
activityActive                -0.02371724 0.04900458
activityInsufficiently_Active  0.03458245 0.10360291
activityInactive               0.06761135 0.12669366

The model suggests, based on these 1133 subjects, that (remember that the baseline category is Highly Active)

  • a 95% confidence (uncertainty) interval for the difference between Active and Highly Active subjects in log(BMI) ranges from -0.024 to 0.049
  • a 95% confidence (uncertainty) interval for the difference between Insufficiently Active and Highly Active subjects in log(BMI) ranges from 0.035 to 0.104
  • a 95% confidence (uncertainty) interval for the difference between Inactive and Highly Active subjects in log(BMI) ranges from 0.068 to 0.127
  • the model accounts for 4.13% of the variation in log(BMI), so that knowing the respondent’s activity level somewhat reduces the size of the prediction errors as compared to an intercept only model that would predict the overall mean log(BMI), regardless of activity level, for all subjects.
  • from the summary of residuals, we see that one subject had a residual of 0.88 - that means they were predicted to have a log(BMI) 0.88 lower than their actual log(BMI) and one subject had a log(BMI) that is 0.76 larger than their actual log(BMI), at the extremes.

5.1.6 Using broom::tidy to explore the coefficients

A better strategy for displaying the coefficients in any regression model is to use the tidy function from the broom package.

term estimate std.error statistic p.value conf.low conf.high
(Intercept) 3.279 0.010 329.833 0.000 3.260 3.299
activityActive 0.013 0.019 0.682 0.495 -0.024 0.049
activityInsufficiently_Active 0.069 0.018 3.928 0.000 0.035 0.104
activityInactive 0.097 0.015 6.453 0.000 0.068 0.127

5.1.7 Using broom::glance to summarize the model’s fit

r.squared adj.r.squared sigma
0.0413 0.0388 0.206
  • The r.squared or \(R^2\) value is interpreted for a linear model as the percentage of variation in the outcome (here, log(bmi)) that is accounted for by the model.
  • The adj.r.squared or adjusted \(R^2\) value incorporates a small penalty for the number of predictors included in the model. Adjusted \(R^2\) is useful for models with more than one predictor, not simple regression models like this one. Like \(R^2\) and most of these other summaries, its primary value comes when making comparisons between models for the same outcome.
  • The sigma or \(\sigma\) is the residual standard error. Doubling this value gives us a good idea of the range of errors made by the model (approximately 95% of the time if the normal distribution assumption for the residuals holds perfectly.)
statistic p.value df logLik
16.21 0 4 186.02
  • The statistic and p.value shown here refer to the ANOVA F test and p value. They test the null hypothesis that the activity information is of no use in separating out the bmi data, or, equivalently, that the true \(R^2\) is 0.
  • The df indicates the model degrees of freedom, and in this case simply specifies the number of parameters fitted attributed to the model. Models that require more df for estimation require larger sample sizes.
  • The logLik is the log likelihood for the model. This is a function of the sample size, but we can compare the fit of multiple models by comparing this value across different models for the same outcome. You want to maximize the log-likelihood.
AIC BIC
-362.03 -336.87
  • The AIC (or Akaike information criterion) and BIC (Bayes information criterion) are also used only to compare models. You want to minimize AIC and BIC in selecting a model. AIC and BIC are unique only up to a constant, so different packages or routines in R may give differing values, but in comparing two models - the difference in AIC (or BIC) should be consistent.

5.1.8 Using broom::augment to make predictions

We can obtain residuals and predicted (fitted) values for the points used to fit the model with augment from the broom package.

log.bmi. activity .fitted .se.fit .resid
3.330 Inactive 3.377 0.011 -0.047
3.138 Inactive 3.377 0.011 -0.239
3.293 Insufficiently_Active 3.349 0.015 -0.055
3.278 Highly_Active 3.279 0.010 -0.002
  • The .fitted value is the predicted value of log(bmi) for this subject.
  • The .se.fit value shows the standard error associated with the fitted value.
  • The .resid is the residual value (observed - fitted log(bmi))
log.bmi. activity .hat .sigma .cooksd .std.resid
3.330 Inactive 0.003 0.206 0.000 -0.227
3.138 Inactive 0.003 0.206 0.001 -1.163
3.293 Insufficiently_Active 0.005 0.206 0.000 -0.270
3.278 Highly_Active 0.002 0.206 0.000 -0.009
  • The .hat value shows the leverage index associated with the observation (this is a function of the predictors - higher leveraged points have more unusual predictor values)
  • The .sigma value shows the estimate of the residual standard deviation if this observation were to be dropped from the model, and thus indexes how much of an outlier this observation’s residual is.
  • The .cooksd or Cook’s distance value shows the influence that the observation has on the model - it is one of a class of leave-one-out diagnostic measures. Larger values of Cook’s distance indicate more influential points.
  • The .std.resid shows the standardized residual (which is designed to have mean 0 and standard deviation 1, facilitating comparisons across models for differing outcomes)

5.2 A Two-Factor ANOVA (without Interaction)

Let’s add race_eth to the predictor set for log(BMI).

Analysis of Variance Table

Response: log(bmi)
            Df Sum Sq Mean Sq F value    Pr(>F)    
activity     3  2.058 0.68603 16.4984 1.701e-10 ***
race_eth     4  0.990 0.24755  5.9533 9.669e-05 ***
Residuals 1125 46.779 0.04158                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Notice that the ANOVA model assesses these variables sequentially, so the SS(activity) = 2.058 is accounted for before we consider the SS(race_eth) = 0.990. Thus, in total, the model accounts for 2.058 + 0.990 = 3.048 of the sums of squares in log(bmi) in these data.

If we flip the order in the model, like this:

Analysis of Variance Table

Response: log(bmi)
            Df Sum Sq Mean Sq F value    Pr(>F)    
race_eth     4  1.121 0.28020  6.7386 2.329e-05 ***
activity     3  1.927 0.64249 15.4514 7.443e-10 ***
Residuals 1125 46.779 0.04158                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  • After flipping the order of the predictors, race_eth accounts for a larger Sum of Squares than it did previously, but activity accounts for a smaller amount, and the total between race_eth and activity remains the same, as 1.121 + 1.927 is still 3.048.

5.2.1 Model Coefficients

The model coefficients are unchanged regardless of the order of the variables in our two-factor ANOVA model.

term estimate std.error conf.low conf.high
(Intercept) 3.268 0.010 3.248 3.289
activityActive 0.012 0.018 -0.024 0.048
activityInsufficiently_Active 0.073 0.018 0.039 0.108
activityInactive 0.092 0.015 0.063 0.122
race_ethBlack non-Hispanic 0.066 0.015 0.036 0.096
race_ethOther race non-Hispanic -0.086 0.042 -0.169 -0.002
race_ethMultiracial non-Hispanic 0.020 0.042 -0.063 0.103
race_ethHispanic 0.012 0.035 -0.057 0.081

The model_5b equation is:

log(BMI) = 3.268
      + 0.012 (activity = Active)
      + 0.073 (activity = Insufficiently Active)
      + 0.092 (activity = Inactive)
      + 0.066 (race_eth = Black non-Hispanic)
      - 0.086 (race_eth = Other race non-Hispanic)
      + 0.020 (race_eth = Multiracial non-Hispanic)
      + 0.012 (race_eth = Hispanic)

and we can make predictions by filling in appropriate 1s and 0s for the indicator variables in parentheses.

For example, the predicted log(BMI) for a White Highly Active person is 3.268, as White and Highly Active are the baseline categories in our two factors.

For all other combinations, we can make predictions as follows:

# A tibble: 20 x 4
   race_eth                 activity              .fitted .se.fit
   <chr>                    <chr>                   <dbl>   <dbl>
 1 White non-Hispanic       Highly_Active            3.27  0.0104
 2 Black non-Hispanic       Highly_Active            3.33  0.0159
 3 Other race non-Hispanic  Highly_Active            3.18  0.0428
 4 Multiracial non-Hispanic Highly_Active            3.29  0.0421
 5 Hispanic                 Highly_Active            3.28  0.0355
 6 White non-Hispanic       Active                   3.28  0.0159
 7 Black non-Hispanic       Active                   3.35  0.0199
 8 Other race non-Hispanic  Active                   3.19  0.0446
 9 Multiracial non-Hispanic Active                   3.30  0.0442
10 Hispanic                 Active                   3.29  0.0369
11 White non-Hispanic       Insufficiently_Active    3.34  0.0149
12 Black non-Hispanic       Insufficiently_Active    3.41  0.0192
13 Other race non-Hispanic  Insufficiently_Active    3.26  0.0425
14 Multiracial non-Hispanic Insufficiently_Active    3.36  0.0437
15 Hispanic                 Insufficiently_Active    3.35  0.0378
16 White non-Hispanic       Inactive                 3.36  0.0121
17 Black non-Hispanic       Inactive                 3.43  0.0160
18 Other race non-Hispanic  Inactive                 3.27  0.0433
19 Multiracial non-Hispanic Inactive                 3.38  0.0430
20 Hispanic                 Inactive                 3.37  0.0355

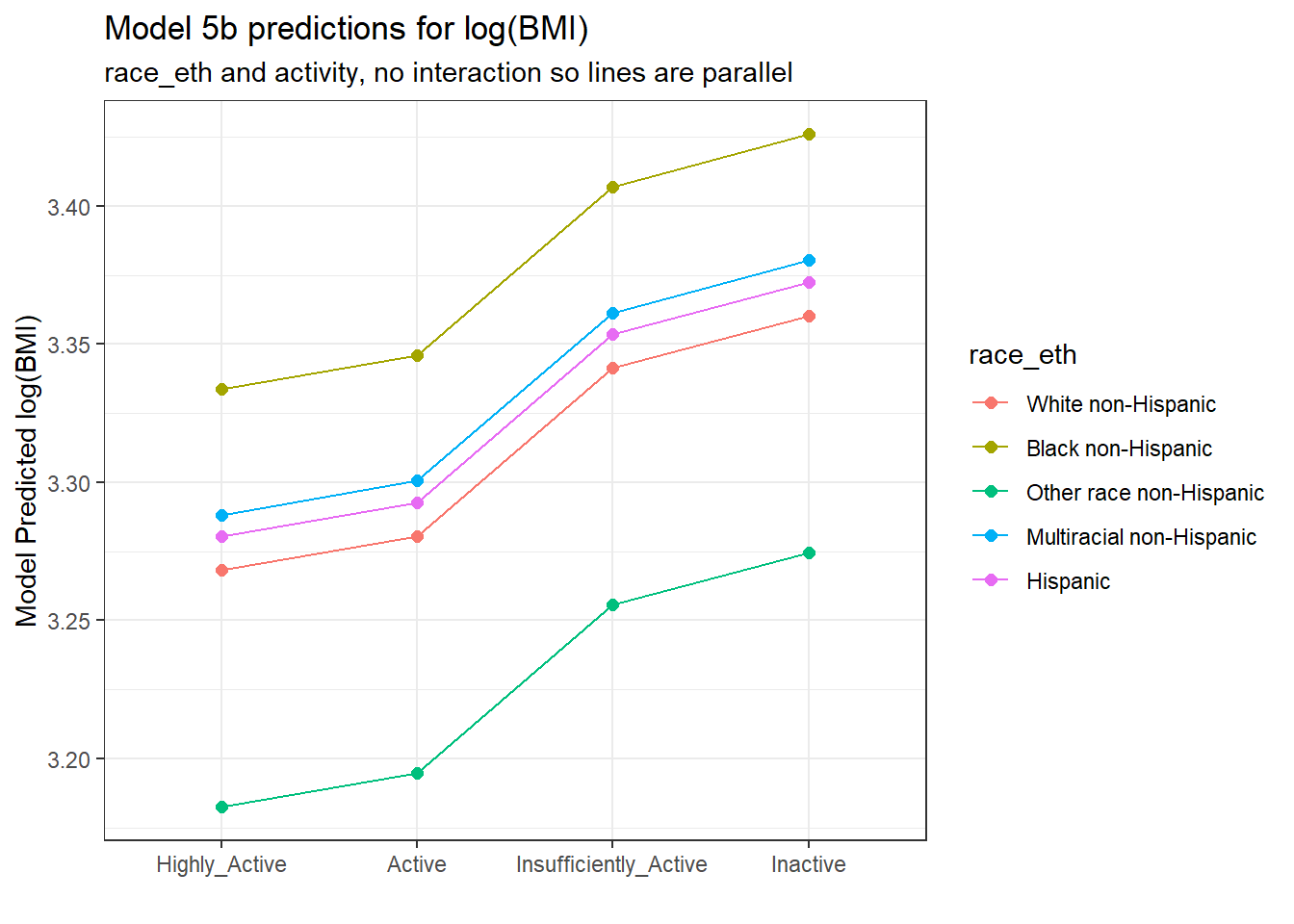
The lines joining the points for each race_eth category are parallel to each other. The groups always hold the same position relative to each other, regardless of their activity levels, and vice versa. There is no interaction in this model allowing the predicted effects of, say, activity on log(BMI) values to differ for the various race_eth groups. To do that, we’d have to fit the two-factor ANOVA model incorporating an interaction term.

5.3 A Two-Factor ANOVA (with Interaction)

Let’s add the interaction of activity and race_eth (symbolized in R by activity * race_eth) to the model for log(BMI).

Analysis of Variance Table

Response: log(bmi)
                    Df Sum Sq Mean Sq F value    Pr(>F)    
activity             3  2.058 0.68603 16.4361 1.867e-10 ***
race_eth             4  0.990 0.24755  5.9309 0.0001008 ***
activity:race_eth   12  0.324 0.02697  0.6462 0.8034404    
Residuals         1113 46.456 0.04174                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The ANOVA model shows that the SS(interaction) = SS(activity:race_eth) is 0.324, and uses 12 degrees of freedom. The model including the interaction term now accounts for 2.058 + 0.990 + 0.324 = 3.372, which is 6.8% of the variation in log(BMI) overall (which is calculated as SS(Total) = 2.058 + 0.990 + 0.324 + 46.456 = 49.828.)

5.3.1 Model Coefficients

The model coefficients now include additional product terms that incorporate indicator variables for both activity and race_eth. For each of the product terms to take effect, both their activity and race_eth status must yield a 1 in the indicator variables.

term estimate std.error conf.low conf.high
(Intercept) 3.264 0.011 3.242 3.287
activityActive 0.020 0.021 -0.021 0.062
activityInsufficiently_Active 0.078 0.020 0.039 0.118
activityInactive 0.097 0.018 0.063 0.132
race_ethBlack non-Hispanic 0.062 0.026 0.011 0.113
race_ethOther race non-Hispanic -0.070 0.078 -0.223 0.083
race_ethMultiracial non-Hispanic 0.067 0.060 -0.051 0.185
race_ethHispanic 0.110 0.060 -0.008 0.228
activityActive:race_ethBlack non-Hispanic -0.002 0.048 -0.097 0.093
activityInsufficiently_Active:race_ethBlack non-Hispanic 0.005 0.046 -0.086 0.096
activityInactive:race_ethBlack non-Hispanic 0.008 0.037 -0.065 0.080
activityActive:race_ethOther race non-Hispanic -0.065 0.165 -0.389 0.259
activityInsufficiently_Active:race_ethOther race non-Hispanic -0.035 0.101 -0.233 0.163
activityInactive:race_ethOther race non-Hispanic 0.033 0.129 -0.221 0.287
activityActive:race_ethMultiracial non-Hispanic -0.208 0.134 -0.470 0.054
activityInsufficiently_Active:race_ethMultiracial non-Hispanic -0.050 0.120 -0.285 0.184
activityInactive:race_ethMultiracial non-Hispanic -0.056 0.110 -0.272 0.160
activityActive:race_ethHispanic -0.104 0.096 -0.291 0.084
activityInsufficiently_Active:race_ethHispanic -0.240 0.214 -0.660 0.179
activityInactive:race_ethHispanic -0.169 0.082 -0.331 -0.008

The model_5c equation is:

log(BMI) = 3.264
  + 0.021 (activity = Active)
  + 0.079 (activity = Insufficiently Active)
  + 0.097 (activity = Inactive)
  + 0.062 (race_eth = Black non-Hispanic)
  - 0.070 (race_eth = Other race non-Hispanic)
  + 0.067 (race_eth = Multiracial non-Hispanic)
  + 0.110 (race_eth = Hispanic)
  - 0.002 (activity = Active)(race_eth = Black non-Hispanic)
  + 0.005 (Insufficiently Active)(Black non-Hispanic)
  + 0.008 (Inactive)(Black non-Hispanic)
  - 0.065 (Active)(Other race non-Hispanic)
  - 0.035 (Insufficiently Active)(Other race non-Hispanic)
  + 0.033 (Inactive)(Other race non-Hispanic)
  - 0.208 (Active)(Multiracial non-Hispanic)
  - 0.050 (Insufficiently Active)(Multiracial non-Hispanic)
  - 0.056 (Inactive)(Multiracial non-Hispanic)
  - 0.104 (Active)(Hispanic)
  - 0.240 (Insufficiently Active)(Hispanic)
  - 0.169 (Inactive)(Hispanic)

and again, we can make predictions by filling in appropriate 1s and 0s for the indicator variables in parentheses.

For example, the predicted log(BMI) for a White Highly Active person is 3.264, as White and Highly Active are the baseline categories in our two factors.

But the predicted log(BMI) for a Hispanic Inactive person would be 3.264 + 0.097 + 0.110 - 0.169 = 3.302.

Again, we’ll plot the predicted log(BMI) predictions for each possible combination.

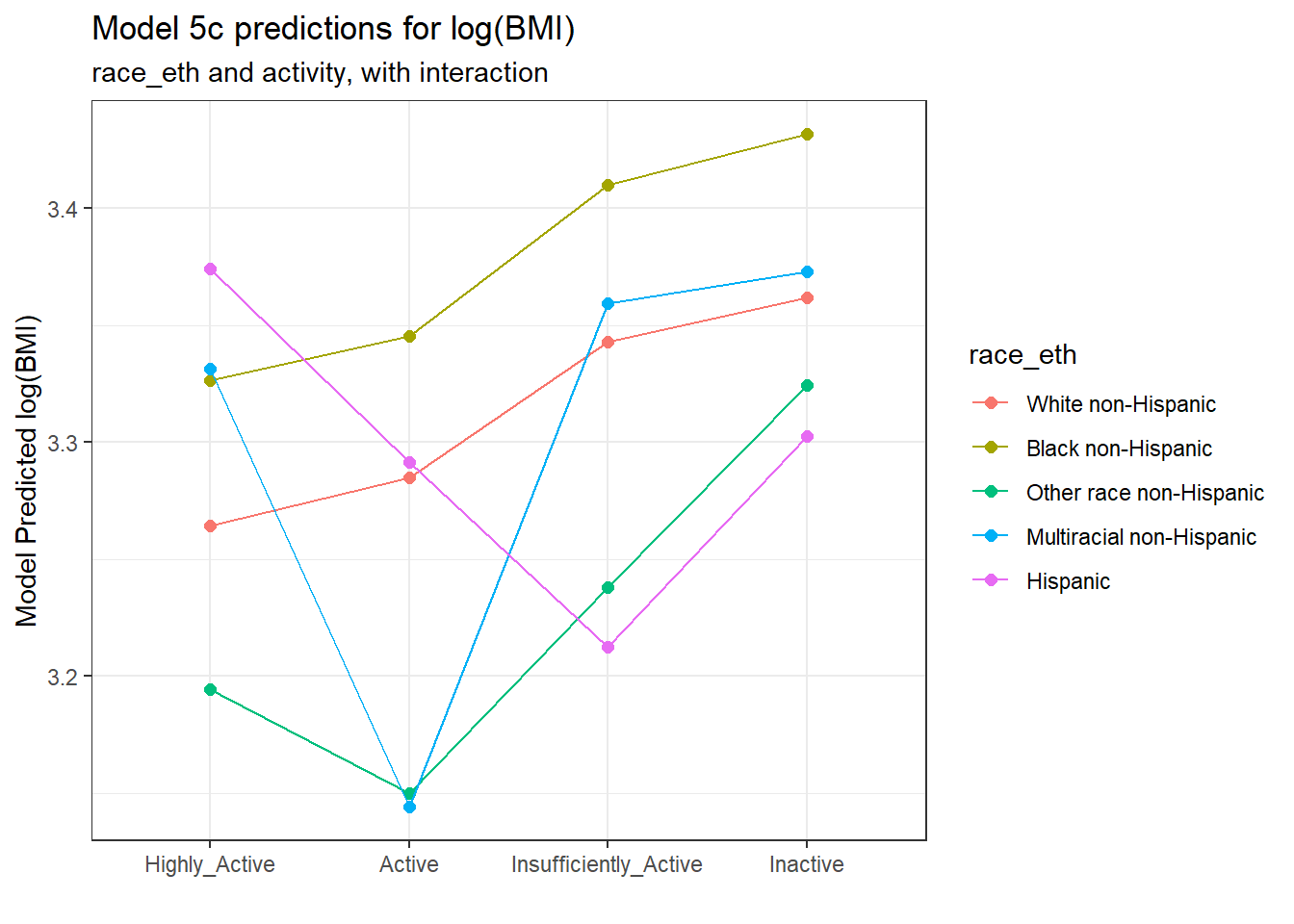
Note that the lines joining the points for each race_eth category are no longer parallel to each other. The race-ethnicity group relative positions on log(BMI) is now changing depending on the activity status.

5.3.2 Is the interaction term necessary?

We can assess this in three ways, in order of importance:

  1. With an interaction plot
  2. By assessing the fraction of the variation in the outcome accounted for by the interaction
  3. By assessing whether the interaction accounts for statistically detectable outcome variation

5.3.2.1 The Interaction Plot

A simple interaction plot is just a plot of the unadjusted outcome means, stratified by the two factors. For example, consider this plot for our two-factor ANOVA model. To obtain this plot, we first summarize the means within each group.

# A tibble: 20 x 5
# Groups:   activity [4]
   activity              race_eth                     n  mean      sd
   <fct>                 <fct>                    <int> <dbl>   <dbl>
 1 Highly_Active         White non-Hispanic         320  3.26  0.176 
 2 Highly_Active         Black non-Hispanic          77  3.33  0.190 
 3 Highly_Active         Other race non-Hispanic      7  3.19  0.198 
 4 Highly_Active         Multiracial non-Hispanic    12  3.33  0.187 
 5 Highly_Active         Hispanic                    12  3.37  0.296 
 6 Active                White non-Hispanic         129  3.28  0.173 
 7 Active                Black non-Hispanic          31  3.35  0.224 
 8 Active                Other race non-Hispanic      2  3.15  0.0845
 9 Active                Multiracial non-Hispanic     3  3.14  0.121 
10 Active                Hispanic                     8  3.29  0.213 
11 Insufficiently_Active White non-Hispanic         150  3.34  0.194 
12 Insufficiently_Active Black non-Hispanic          35  3.41  0.213 
13 Insufficiently_Active Other race non-Hispanic     11  3.24  0.137 
14 Insufficiently_Active Multiracial non-Hispanic     4  3.36  0.374 
15 Insufficiently_Active Hispanic                     1  3.21 NA     
16 Inactive              White non-Hispanic         225  3.36  0.238 
17 Inactive              Black non-Hispanic          83  3.43  0.247 
18 Inactive              Other race non-Hispanic      4  3.32  0.238 
19 Inactive              Multiracial non-Hispanic     5  3.37  0.129 
20 Inactive              Hispanic                    14  3.30  0.264

The interaction plot suggests that there is a modest interaction here. The White non-Hispanic and Black non-Hispanic groups appear pretty parallel (and they are the two largest groups) and Other race non-Hispanic has a fairly similar pattern, but the other two groups (Hispanic and Multiracial non-Hispanic) bounce around quite a bit based on activity level.

An alternative would be to include a small “dodge” for each point and include error bars (means \(\pm\) standard deviation) for each combination.

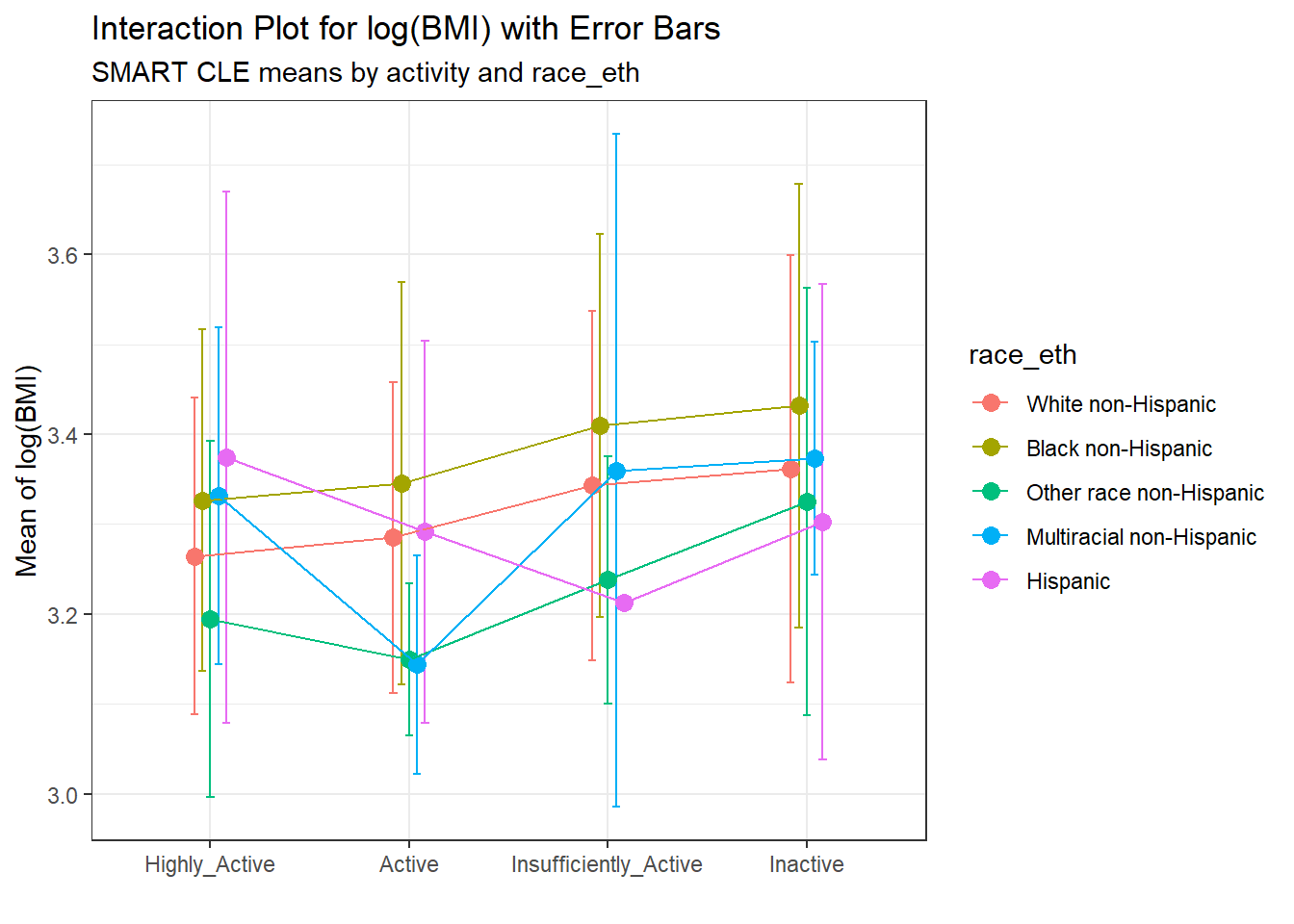
Here, we see a warning flag because we have one combination (which turns out to be Insufficiently Active and Hispanic) with only one observation in it, so a standard deviation cannot be calculated. In general, I’ll stick with the simpler means plot most of the time.

5.3.2.2 Does the interaction account for substantial variation?

In this case, we can look at the fraction of the overall sums of squares accounted for by the interaction.

Analysis of Variance Table

Response: log(bmi)
                    Df Sum Sq Mean Sq F value    Pr(>F)    
activity             3  2.058 0.68603 16.4361 1.867e-10 ***
race_eth             4  0.990 0.24755  5.9309 0.0001008 ***
activity:race_eth   12  0.324 0.02697  0.6462 0.8034404    
Residuals         1113 46.456 0.04174                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Here we have

\[ \eta^2(Interaction) = \frac{0.324}{2.058+0.990+0.324+46.456} = 0.0065 \]

so the interaction accounts for 0.65% of the variation in bmi. That looks pretty modest.

5.3.2.3 Does the interaction account for statistically detectable variation?

We can test this directly with the p value from the ANOVA table, which shows p = 0.803, which is far above any of our usual standards for a statistically detectable effect.

On the whole, I don’t think the interaction term is especially helpful in improving this model.

In the next chapter, we’ll look at two different examples of ANOVA models, now in more designed experiments. We’ll also add some additional details on how the analyses might proceed.

We’ll return to the SMART CLE data later in these Notes.