Chapter 3 Dealing with Missingness: Single Imputation

3.1 Selecting Some Variables from the smart_cle data

The smart_cle.Rds data file available on the Data and Code page of our website describes information on 99 variables for 1133 respondents to the BRFSS 2017, who live in the Cleveland-Elyria, OH, Metropolitan Statistical Area. The variables in the smart_cle1.csv file are listed below, along with the items that generate these responses.

Variable Description
SEQNO respondent identification number (all begin with 2016)
physhealth Now thinking about your physical health, which includes physical illness and injury, for how many days during the past 30 days was your physical health not good?
genhealth Would you say that in general, your health is … (five categories: Excellent, Very Good, Good, Fair or Poor)
bmi Body mass index, in kg/m2
age_imp Age, imputed, in years
female Sex, 1 = female, 0 = male
race_eth Race and Ethnicity, in five categories
internet30 Have you used the internet in the past 30 days? (1 = yes, 0 = no)
smoke100 Have you smoked at least 100 cigarettes in your life? (1 = yes, 0 = no)
activity Physical activity (Highly Active, Active, Insufficiently Active, Inactive)
drinks_wk On average, how many drinks of alcohol do you consume in a week?
veg_day How many servings of vegetables do you consume per day, on average? 
Classes 'tbl_df', 'tbl' and 'data.frame':   1133 obs. of  12 variables:
 $ SEQNO     : num  2.02e+09 2.02e+09 2.02e+09 2.02e+09 2.02e+09 ...
 $ physhealth: num  4 0 0 0 0 2 2 0 0 0 ...
 $ genhealth : Factor w/ 5 levels "1_Excellent",..: 1 1 3 3 3 2 3 2 4 1 ...
 $ bmi       : num  NA 23.1 26.9 26.5 24.2 ...
 $ age_imp   : num  51 28 37 36 88 43 23 34 58 54 ...
 $ female    : num  1 1 1 1 0 0 0 0 0 1 ...
 $ race_eth  : Factor w/ 5 levels "White non-Hispanic",..: 1 1 3 1 1 1 1 3 2 1 ...
 $ internet30: num  1 1 0 1 1 1 1 1 1 1 ...
 $ smoke100  : num  1 0 0 1 1 1 0 0 0 1 ...
 $ activity  : Factor w/ 4 levels "Highly_Active",..: 4 4 3 1 1 NA 1 1 1 1 ...
 $ drinks_wk : num  0.7 0 0 4.67 0.93 0 2 0 0 0.47 ...
 $ veg_day   : num  NA 3 4.06 2.07 1.31 NA 1.57 0.83 0.49 1.72 ...

3.2 smart_cle1: Seeing our Missing Data

The naniar package provides several useful functions for summarizing missingness in our data set. Like all tidy data sets, our smart_cle1 tibble contains rows which describe observations, sometimes called cases, and also contains columns which describe variables.

Overall, there are 1133 cases, and 1133 observations in our smart_cle1 tibble.

  • We can obtain a count of the number of missing cells in the entire tibble.
[1] 479
  • We can use the miss_var_summary function to get a sorted table of each variable by number missing.
variable n_miss pct_miss
activity 109 9.6204766
veg_day 101 8.9143866
bmi 91 8.0317741
drinks_wk 66 5.8252427
smoke100 40 3.5304501
race_eth 26 2.2947926
physhealth 24 2.1182701
age_imp 11 0.9708738
internet30 7 0.6178288
genhealth 4 0.3530450
SEQNO 0 0.0000000
female 0 0.0000000
  • Or we can use the miss_var_table function to tabulate the number of variables that have each observed level of missingness.
# A tibble: 11 x 3
   n_miss_in_var n_vars pct_vars
           <int>  <int>    <dbl>
 1             0      2    16.7 
 2             4      1     8.33
 3             7      1     8.33
 4            11      1     8.33
 5            24      1     8.33
 6            26      1     8.33
 7            40      1     8.33
 8            66      1     8.33
 9            91      1     8.33
10           101      1     8.33
11           109      1     8.33
  • Or we can get a count for a specific variable, like activity:
[1] 109
  • We can also use prop_miss_case or pct_miss_case to specify the proportion (or percentage) of missing observations across an entire data set, or within a specific variable.
[1] 0.2127096
[1] 9.620477
  • We can also use prop_miss_var or pct_miss_var to specify the proportion (or percentage) of variables with missing observations across an entire data set.
[1] 0.8333333
[1] 83.33333
  • We use miss_case_table to identify the number of missing values for each of the cases (rows) in our tibble.
# A tibble: 7 x 3
  n_miss_in_case n_cases pct_cases
           <int>   <int>     <dbl>
1              0     892    78.7  
2              1     129    11.4  
3              2      51     4.50 
4              3      22     1.94 
5              4      21     1.85 
6              5      10     0.883
7              6       8     0.706
  • Use miss_case_summary to specify individual observations and count their missing values.
# A tibble: 1,133 x 3
    case n_miss pct_miss
   <int>  <int>    <dbl>
 1    17      6     50  
 2    42      6     50  
 3   254      6     50  
 4   425      6     50  
 5   521      6     50  
 6   729      6     50  
 7   757      6     50  
 8  1051      6     50  
 9    89      5     41.7
10    94      5     41.7
# ... with 1,123 more rows

The case numbers identified here are row numbers. Extract the data for case 17, for instance, with the slice function.

# A tibble: 1 x 12
   SEQNO physhealth genhealth   bmi age_imp female race_eth internet30 smoke100
   <dbl>      <dbl> <fct>     <dbl>   <dbl>  <dbl> <fct>         <dbl>    <dbl>
1 2.02e9          0 1_Excell~    NA      50      0 White n~         NA       NA
# ... with 3 more variables: activity <fct>, drinks_wk <dbl>, veg_day <dbl>

3.2.1 Plotting Missingness

The gg_miss_var function plots the number of missing observations in each variable in our data set.

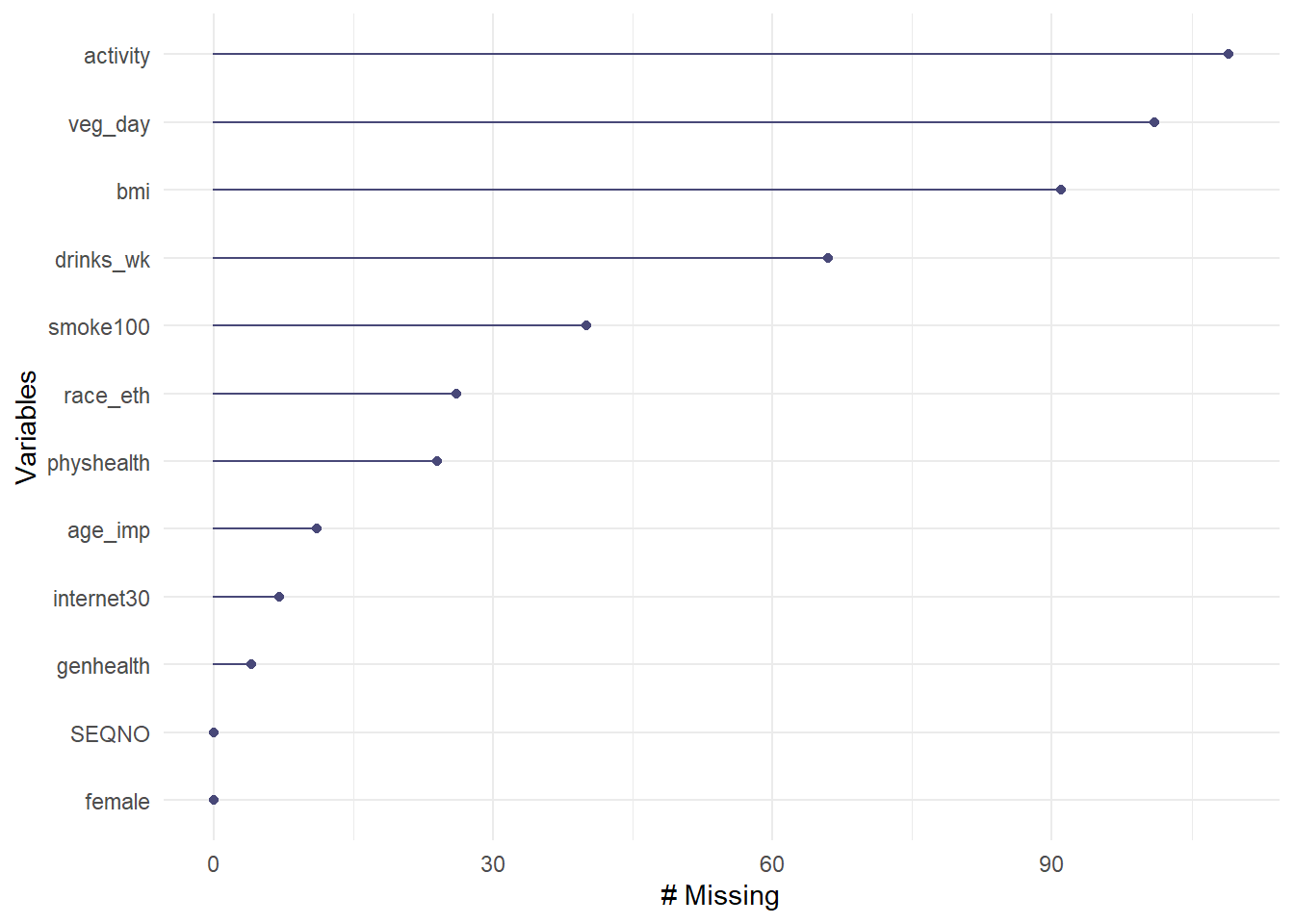
So the most commonly missing variable is activity which, as we’ve seen, has 109 missing values.

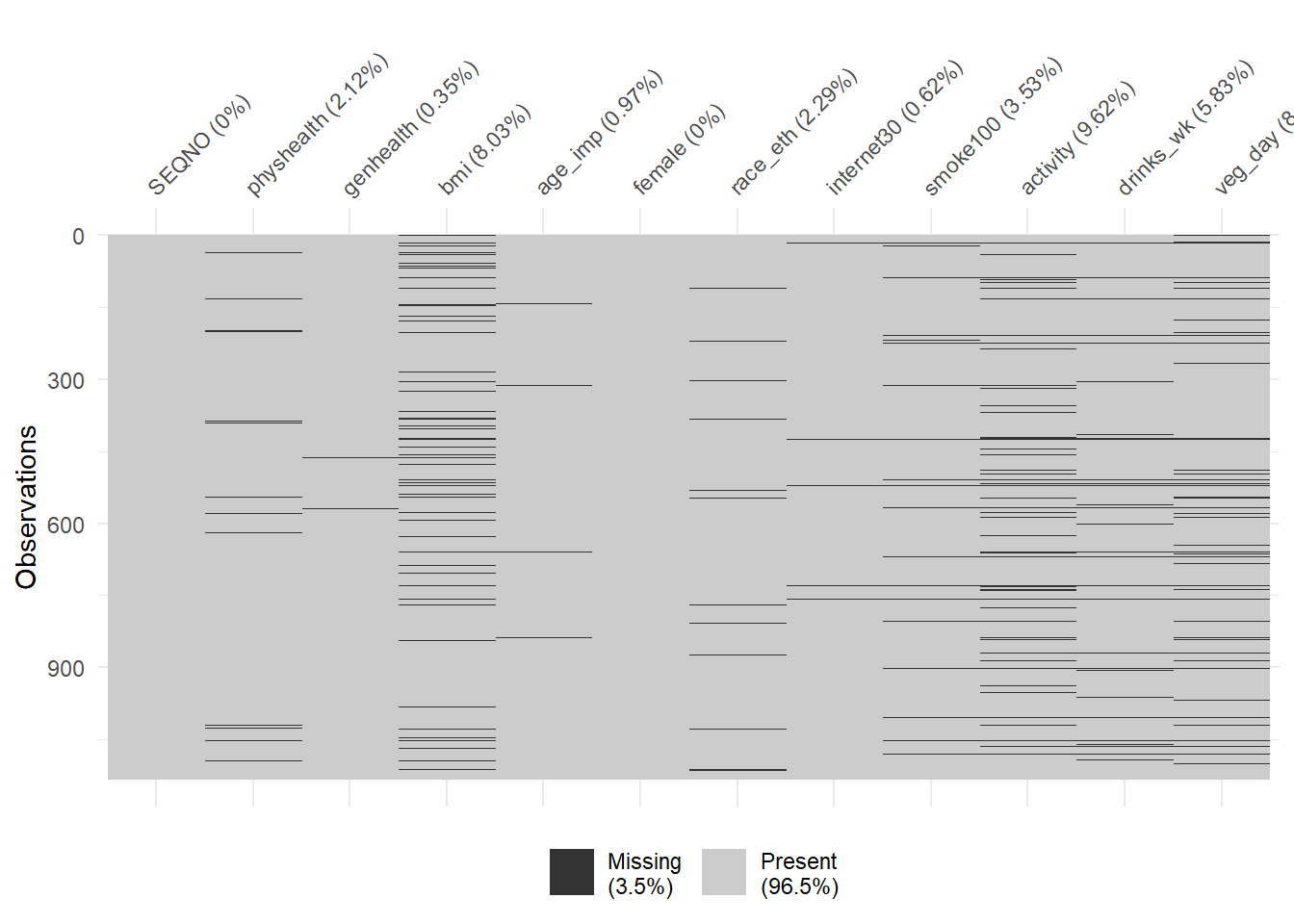
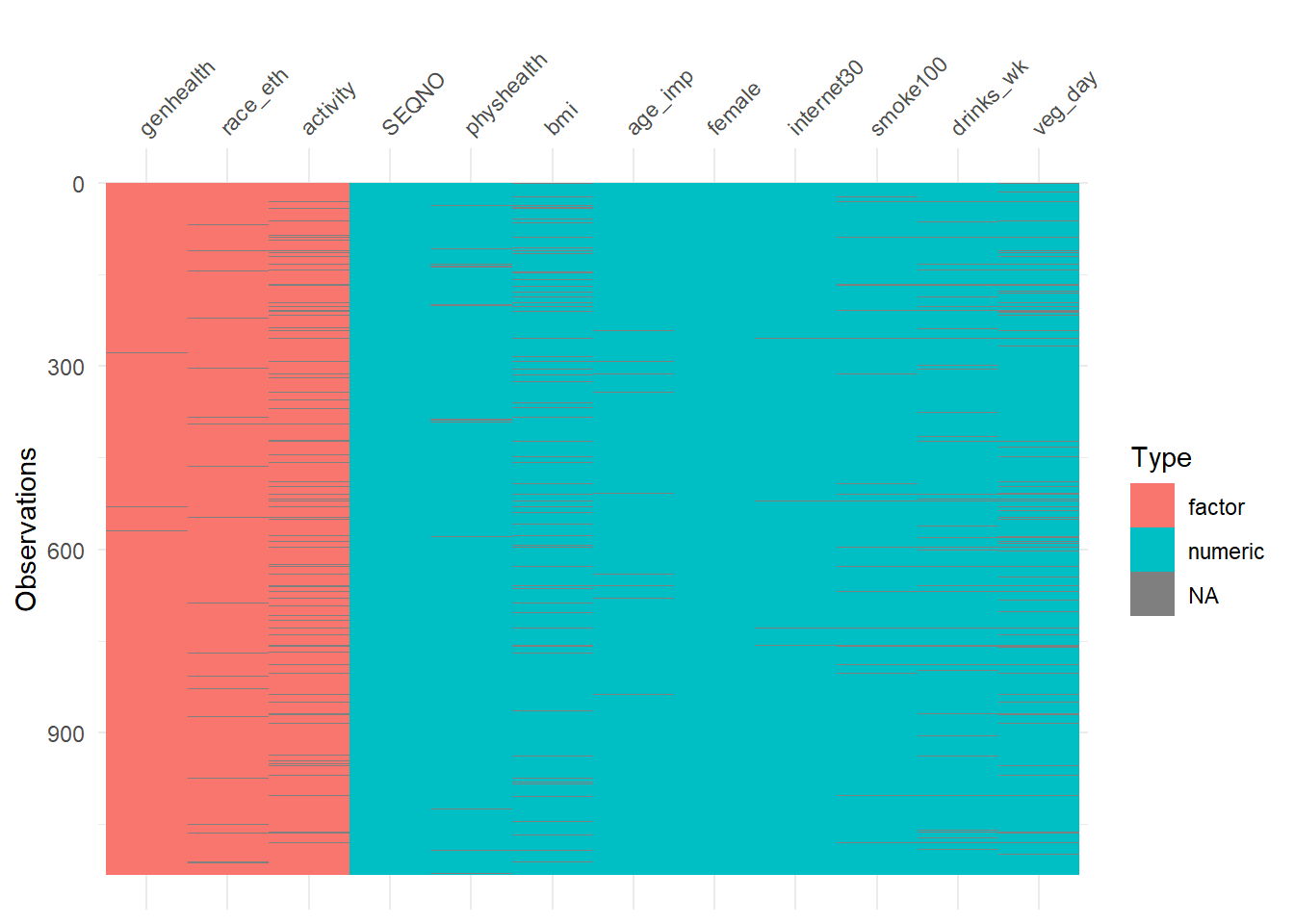
To get a general sense of the missingness in our data, we might use either the vis_dat or the vis_miss function from the visdat package.

3.3 Missing-data mechanisms

My source for this description of mechanisms is Chapter 25 of Gelman and Hill (2007), and that chapter is available at this link.

  1. MCAR = Missingness completely at random. A variable is missing completely at random if the probability of missingness is the same for all units, for example, if for each subject, we decide whether to collect the diabetes status by rolling a die and refusing to answer if a “6” shows up. If data are missing completely at random, then throwing out cases with missing data does not bias your inferences.
  2. Missingness that depends only on observed predictors. A more general assumption, called missing at random or MAR, is that the probability a variable is missing depends only on available information. Here, we would have to be willing to assume that the probability of nonresponse to diabetes depends only on the other, fully recorded variables in the data. It is often reasonable to model this process as a logistic regression, where the outcome variable equals 1 for observed cases and 0 for missing. When an outcome variable is missing at random, it is acceptable to exclude the missing cases (that is, to treat them as NA), as long as the regression controls for all the variables that affect the probability of missingness.
  3. Missingness that depends on unobserved predictors. Missingness is no longer “at random” if it depends on information that has not been recorded and this information also predicts the missing values. If a particular treatment causes discomfort, a patient is more likely to drop out of the study. This missingness is not at random (unless “discomfort” is measured and observed for all patients). If missingness is not at random, it must be explicitly modeled, or else you must accept some bias in your inferences.
  4. Missingness that depends on the missing value itself. Finally, a particularly difficult situation arises when the probability of missingness depends on the (potentially missing) variable itself. For example, suppose that people with higher earnings are less likely to reveal them.

Essentially, situations 3 and 4 are referred to collectively as non-random missingness, and cause more trouble for us than 1 and 2.

3.4 Options for Dealing with Missingness

There are several available methods for dealing with missing data that are MCAR or MAR, but they basically boil down to:

  • Complete Case (or Available Case) analyses
  • Single Imputation
  • Multiple Imputation

3.5 Complete Case (and Available Case) analyses

In Complete Case analyses, rows containing NA values are omitted from the data before analyses commence. This is the default approach for many statistical software packages, and may introduce unpredictable bias and fail to include some useful, often hard-won information.

  • A complete case analysis can be appropriate when the number of missing observations is not large, and the missing pattern is either MCAR (missing completely at random) or MAR (missing at random.)
  • Two problems arise with complete-case analysis:
    1. If the units with missing values differ systematically from the completely observed cases, this could bias the complete-case analysis.
    2. If many variables are included in a model, there may be very few complete cases, so that most of the data would be discarded for the sake of a straightforward analysis.
  • A related approach is available-case analysis where different aspects of a problem are studied with different subsets of the data, perhaps identified on the basis of what is missing in them.

3.6 Single Imputation

In single imputation analyses, NA values are estimated/replaced one time with one particular data value for the purpose of obtaining more complete samples, at the expense of creating some potential bias in the eventual conclusions or obtaining slightly less accurate estimates than would be available if there were no missing values in the data.

  • A single imputation can be just a replacement with the mean or median (for a quantity) or the mode (for a categorical variable.) However, such an approach, though easy to understand, underestimates variance and ignores the relationship of missing values to other variables.
  • Single imputation can also be done using a variety of models to try to capture information about the NA values that are available in other variables within the data set.
  • The simputation package can help us execute single imputations using a wide variety of techniques, within the pipe approach used by the tidyverse. Another approach I have used in the past is the mice package, which can also perform single imputations.

3.7 Multiple Imputation

Multiple imputation, where NA values are repeatedly estimated/replaced with multiple data values, for the purpose of obtaining mode complete samples and capturing details of the variation inherent in the fact that the data have missingness, so as to obtain more accurate estimates than are possible with single imputation.

  • We’ll postpone the discussion of multiple imputation for a while.

3.8 Approach 1: Building a Complete Case Analysis: smart_cle1_cc

In the 431 course, we usually dealt with missing data by restricting our analyses to respondents with complete data on all variables. Let’s start by doing that here. We’ll create a new tibble called smart_cle1_cc which includes all respondents with complete data on all of these variables.

[1] 892  12

Our smart_cle1_cc tibble now has many fewer observations than its predecessors, but all of the variables in this complete cases tibble have no missing observations.

Data Set Rows Columns Missingness?
smart_cle 1133 99 Quite a bit.
smart_cle1 1133 12 Quite a bit.
smart_cle1_cc 892 12 None.

3.9 Approach 2: Single Imputation to create smart_cle1_sh

Next, we’ll create a data set which has all of the rows in the original smart_cle1 tibble, but deals with missingness by imputing (estimating / filling in) new values for each of the missing values. To do this, we’ll make heavy use of the simputation package in R.

The simputation package is designed for single imputation work. Note that we’ll eventually adopt a multiple imputation strategy in some of our modeling work, and we’ll use some specialized tools to facilitate that later.

To begin, we’ll create a “shadow” in our tibble to track what we’ll need to impute.

 [1] "SEQNO"         "physhealth"    "genhealth"     "bmi"          
 [5] "age_imp"       "female"        "race_eth"      "internet30"   
 [9] "smoke100"      "activity"      "drinks_wk"     "veg_day"      
[13] "SEQNO_NA"      "physhealth_NA" "genhealth_NA"  "bmi_NA"       
[17] "age_imp_NA"    "female_NA"     "race_eth_NA"   "internet30_NA"
[21] "smoke100_NA"   "activity_NA"   "drinks_wk_NA"  "veg_day_NA"

Note that the bind_shadow() function doubles the number of variables in our tibble, specifically by creating a new variable for each that takes the value !NA or NA. For example, consider

# A tibble: 5 x 3
  activity              activity_NA     n
  <fct>                 <fct>       <int>
1 Highly_Active         !NA           338
2 Active                !NA           173
3 Insufficiently_Active !NA           201
4 Inactive              !NA           312
5 <NA>                  NA            109

The activity_NA variable takes the value !NA (meaning not missing) when the value of the activity variable is known, and takes the value NA for observations where the activity variable is missing. This background tracking will be helpful to us when we try to assess the impact of imputation on some of our summaries.

3.9.1 What Type of Missingness Do We Have?

There are three types of missingness that we might assume in any given setting: missing completely at random (MCAR), missing at random (MAR) and missing not at random (MNAR). Together, MCAR and MAR are sometimes called ignorable non-response, which essentially means that imputation provides a way to useful estimates. MNAR or missing NOT at random is sometimes called non-ignorable missingness, implying that even high-quality imputation may not be sufficient to provide useful information to us.

Missing Completely at Random means that the missing data points are a random subset of the data. Essentially, there is nothing that makes some data more likely to be missing than others. If the data truly match the standard for MCAR, then a complete-case analysis will be about as good as an analysis after single or multiple imputation.

Missing at Random means that there is a systematic relationship between the observed data and the missingness mechanism. Another way to say this is that the missing value is not related to the reason why it is missing, but is related to the other variables collected in the study. The implication is that the missingness can be accounted for by studying the variables with complete information. Imputation strategies can be very helpful here, incorporating what we know (or think we know) about the relationships between the results that are missing and the results that we see.

  • Wikipedia provides a nice example. If men are less likely to fill in a depression survey, but this has nothing to do with their level of depression after accounting for the fact that they are male, then the missingess can be assumed MAR.
  • Determining whether missingness is MAR or MNAR can be tricky. We’ll spend more time discussing this later.

Missing NOT at Random means that the missing value is related to the reason why it is missing.

  • Continuing the Wikipedia example, if men failed to fill in a depression survey because of their level of depression, then this would be MNAR.

  • Single imputation is most helpful in the MAR situation, although it is also appropriate when we assume MCAR.

  • Multiple imputation will, similarly, be more helpful in MCAR and MAR situations than when data are missing NOT at random.

It’s worth noting that many people are unwilling to impute values for outcomes or key predictors in a modeling setting, but are happy to impute for less important covariates. For now, we’ll assume MCAR or MAR for all of the missingness in our smart_cle1 data, which will allow us to adopt a single imputation strategy.

3.9.2 Single imputation into smart_cle1_sh

Which variables in smart_cle1_sh contain missing data?

# A tibble: 24 x 3
   variable   n_miss pct_miss
   <chr>       <int>    <dbl>
 1 activity      109    9.62 
 2 veg_day       101    8.91 
 3 bmi            91    8.03 
 4 drinks_wk      66    5.83 
 5 smoke100       40    3.53 
 6 race_eth       26    2.29 
 7 physhealth     24    2.12 
 8 age_imp        11    0.971
 9 internet30      7    0.618
10 genhealth       4    0.353
# ... with 14 more rows

We will impute these variables using several different strategies, all supported nicely by the simputation package.

These include imputation methods based solely on the distribution of the complete cases of the variable being imputed.

  • impute_median: impute the median value of all non-missing observations into the missing values for the variable
  • impute_rhd: random “hot deck” imputation involves drawing at random from the complete cases for that variable

Also available are imputation strategies that impute predicted values from models using other variables in the data set besides the one being imputed.

  • impute_pmm: imputation using predictive mean matching
  • impute_rlm: imputation using robust linear models
  • impute_cart: imputation using classification and regression trees
  • impute_knn: imputation using k-nearest neighbors methods

3.9.3 Imputing Binary Categorical Variables

Here, we’ll arbitrarily impute our 1/0 variables as follows:

  • For internet30 we’ll use the impute_rhd approach to draw a random observation from the existing set of 1s and 0s in the complete internet30 data.
  • For smoke100 we’ll use a method called predictive mean matching (impute_pmm) which takes the result from a model based on the (imputed) internet30 value and whether or not the subject is female, and converts it to the nearest value in the observed smoke100 data. This is a good approach for imputing discrete variables.

These are completely arbitrary choices, for demonstration purposes.

# A tibble: 4 x 3
  smoke100 smoke100_NA     n
     <dbl> <fct>       <int>
1        0 !NA           579
2        0 NA             21
3        1 !NA           514
4        1 NA             19
# A tibble: 4 x 3
  internet30 internet30_NA     n
       <dbl> <fct>         <int>
1          0 !NA             207
2          0 NA                1
3          1 !NA             919
4          1 NA                6

Other approaches that may be used with 1/0 variables include impute_knn and impute_pmm.

3.9.4 Imputing Quantitative Variables

We’ll demonstrate a different approach for imputing each of the quantitative variables with missing observations. Again, we’re making purely arbitrary decisions here about what to include in each imputation. In practical work, we’d want to be a bit more thoughtful about this.

Note that I’m choosing to use impute_pmm with the physhealth and age_imp variables. This is (in part) because I want my imputations to be integers, as the other observations are for those variables. impute_rhd would also accomplish this.

3.9.5 Imputation Results

Let’s plot a few of these results, so we can see what imputation has done to the distribution of these quantities.

  1. veg_day

  veg_day_NA  min     Q1 median   Q3  max     mean       sd    n missing
1        !NA 0.00 1.2675   1.72 2.42 7.49 1.912548 1.038403 1032       0
2         NA 0.26 1.3400   1.86 2.72 5.97 2.085050 1.062316  101       0
  1. drinks_wk for which we imputed the median value…

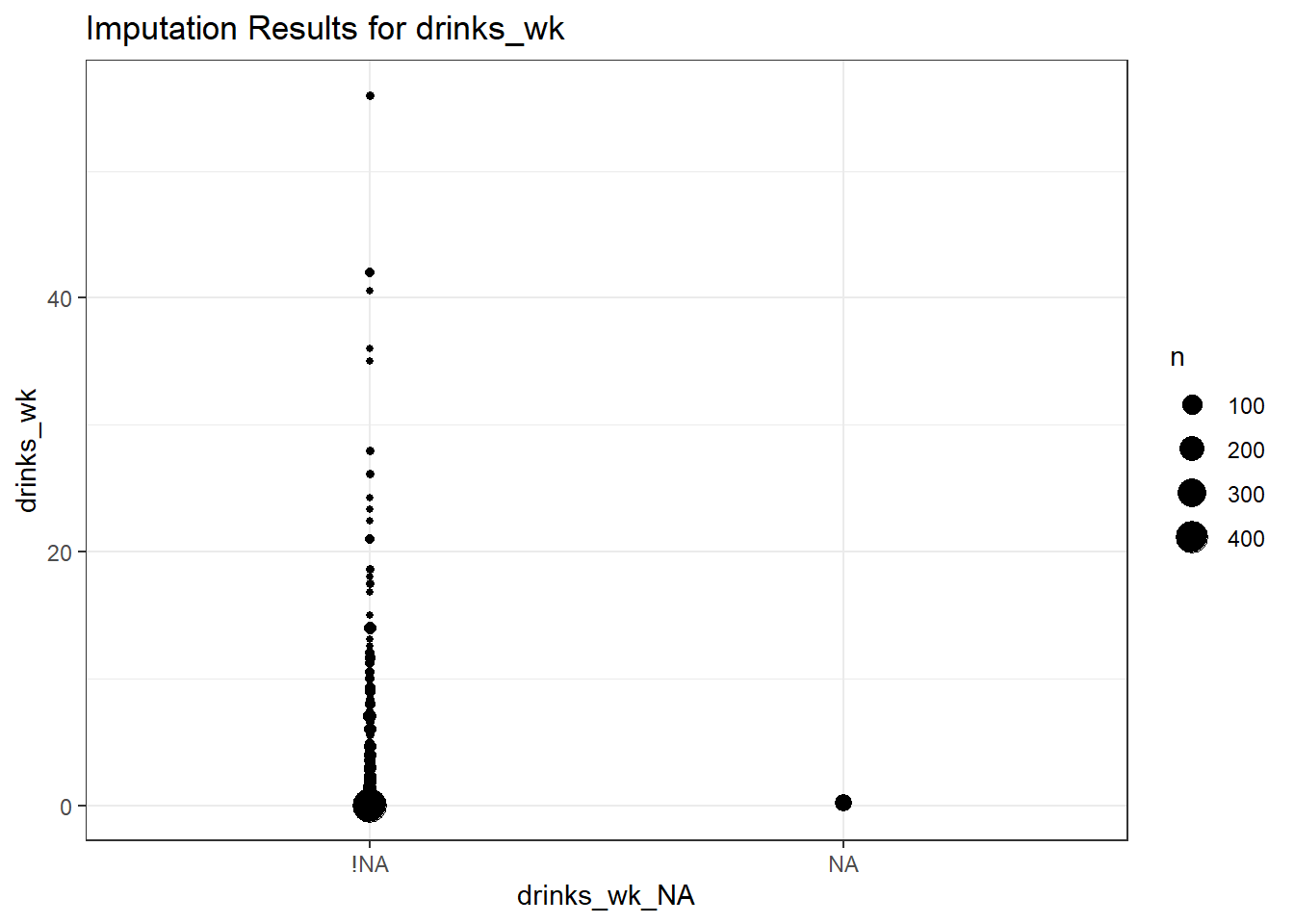
 drinks_wk  n percent
      0.23 66       1
  1. physhealth, a count between 0 and 30…
Picking joint bandwidth of 0.426

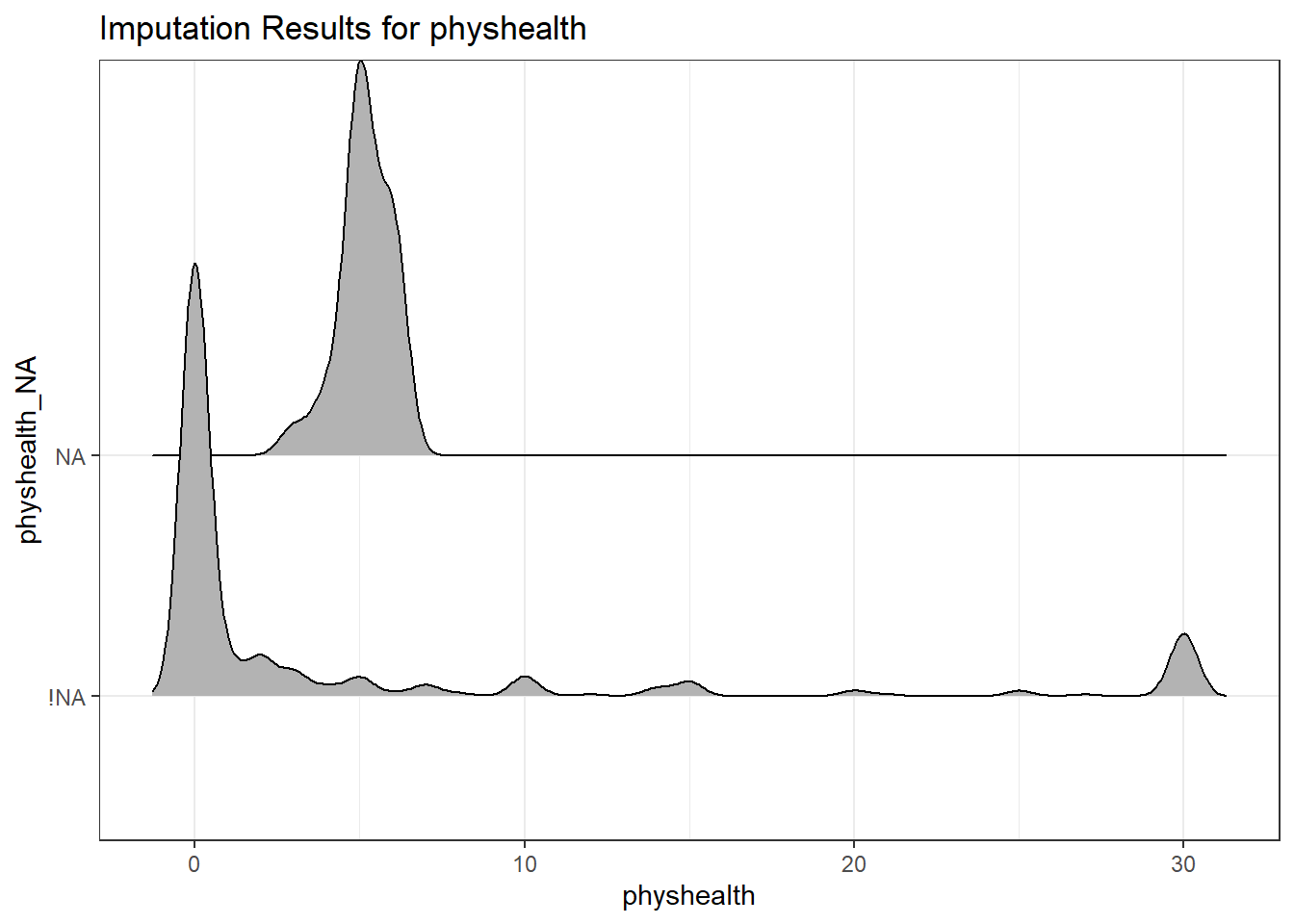
 physhealth  n    percent
          3  1 0.04166667
          4  2 0.08333333
          5 13 0.54166667
          6  8 0.33333333
  1. age_imp, in (integer) years

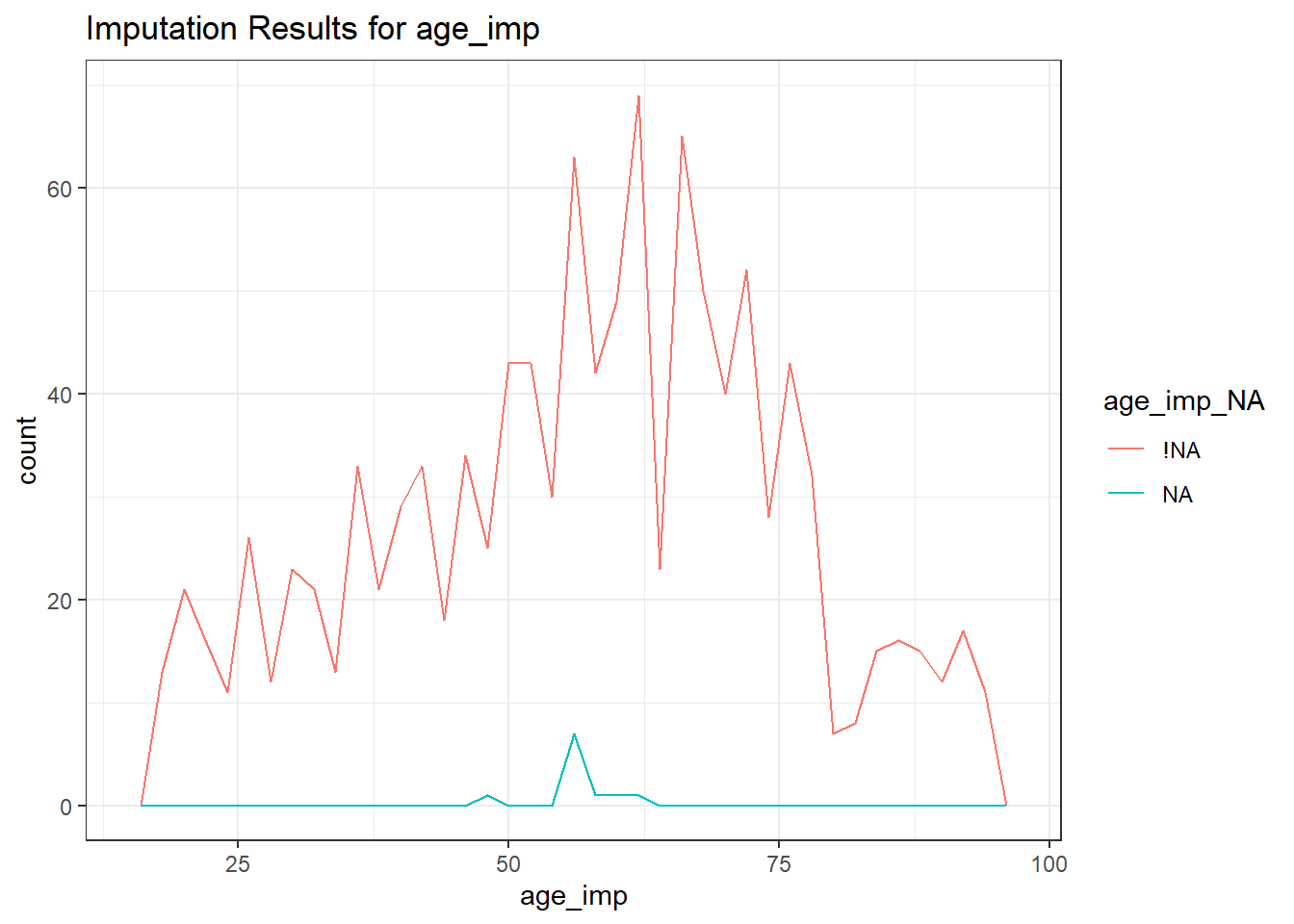
 age_imp n    percent
      48 1 0.09090909
      57 7 0.63636364
      58 1 0.09090909
      61 1 0.09090909
      63 1 0.09090909
  1. bmi or body mass index

  bmi_NA      min       Q1  median      Q3      max     mean        sd    n
1    !NA 13.30000 24.11000 27.3000 31.6800 70.56000 28.41404 6.6298796 1042
2     NA 27.06952 27.06952 27.5045 27.6679 30.76933 27.66257 0.8987429   91
  missing
1       0
2       0

3.9.6 Imputing Multi-Categorical Variables

The three multi-categorical variables we have left to impute are activity, race_eth and genhealth, and each is presented as a factor in R, rather than as a character variable.

We’ll arbitrarily decide to impute

  • activity and genhealth with a classification tree using physhealth, bmi and smoke100,
  • and then impute race_eth with a random draw from the distribution of complete cases.

Let’s check our results.

# A tibble: 6 x 3
  activity_NA activity                  n
  <fct>       <fct>                 <int>
1 !NA         Highly_Active           338
2 !NA         Active                  173
3 !NA         Insufficiently_Active   201
4 !NA         Inactive                312
5 NA          Highly_Active            90
6 NA          Inactive                 19
# A tibble: 9 x 3
  race_eth_NA race_eth                     n
  <fct>       <fct>                    <int>
1 !NA         White non-Hispanic         805
2 !NA         Black non-Hispanic         222
3 !NA         Other race non-Hispanic     24
4 !NA         Multiracial non-Hispanic    22
5 !NA         Hispanic                    34
6 NA          White non-Hispanic          19
7 NA          Black non-Hispanic           4
8 NA          Multiracial non-Hispanic     2
9 NA          Hispanic                     1
# A tibble: 7 x 3
  genhealth_NA genhealth       n
  <fct>        <fct>       <int>
1 !NA          1_Excellent   164
2 !NA          2_VeryGood    383
3 !NA          3_Good        364
4 !NA          4_Fair        158
5 !NA          5_Poor         60
6 NA           2_VeryGood      3
7 NA           3_Good          1

And now, we should have no missing values in the data, at all.

# A tibble: 1 x 3
  n_miss_in_case n_cases pct_cases
           <int>   <int>     <dbl>
1              0    1133       100

References

Gelman, Andrew, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. New York: Cambridge University Press.