Chapter 16 Multiple Imputation and Linear Regression

16.1 Developing a `smart_16` data set

In this chapter, we’ll return to the smart_ohio file based on data from BRFSS 2017 that we built and cleaned back at the start of these Notes.

smart_ohio <- readRDS(here("data", "smart_ohio.Rds"))

We’re going to look at a selection of variables from this tibble, among subjects who have been told they have diabetes, and who also provided a response to our physhealth (Number of Days Physical Health Not Good) variable, which asks “Now thinking about your physical health, which includes physical illness and injury, for how many days during the past 30 days was your physical health not good?” We’ll build two models. In this chapter, we’ll look at a linear model for physhealth and in the next chapter, we’ll look at a logistic regression describing whether or not the subject’s physhealth response was at least 1.

smart_16 <- smart_ohio %>%
    filter(dm_status == "Diabetes") %>%
    filter(complete.cases(physhealth)) %>%
    mutate(bad_phys = ifelse(physhealth > 0, 1, 0),
           comor = hx_mi + hx_chd + hx_stroke + hx_asthma +
               hx_skinc + hx_otherc + hx_copd + hx_arthr) %>%
    select(SEQNO, mmsa, physhealth, bad_phys, age_imp, smoke100,
           comor, hx_depress, bmi, activity)

The variables included in this smart_16 tibble are:

Variable	Description
`SEQNO`	respondent identification number (all begin with 2016)
`mmsa`
`physhealth`	Now thinking about your physical health, which includes physical illness and injury, for how many days during the past 30 days was your physical health not good?
`bad_phys`	Is `physhealth` 1 or more?
`age_imp`	Age in years (imputed from age categories)
`smoke100`	Have you smoked at least 100 cigarettes in your life? (1 = yes, 0 = no)
`hx_depress`	Has a doctor, nurse, or other health professional ever told you that you have a depressive disorder, including depression, major depression, dysthymia, or minor depression?
`bmi`	Body mass index, in kg/m²
`activity`	Physical activity (Highly Active, Active, Insufficiently Active, Inactive)
`comor`	Sum of 8 potential groups of comorbidities (see below)

The comor variable is the sum of the following 8 variables, each of which is measured on a 1 = Yes, 0 = No scale, and begin with “Has a doctor, nurse, or other health professional ever told you that you had …”

hx_mi: a heart attack, also called a myocardial infarction?
hx_chd: angina or coronary heart disease?
hx_stroke: a stroke?
hx_asthma: asthma?
hx_skinc: skin cancer?
hx_otherc: any other types of cancer?
hx_copd: Chronic Obstructive Pulmonary Disease or COPD, emphysema or chronic bronchitis?
hx_arthr: some form of arthritis, rheumatoid arthritis, gout, lupus, or fibromyalgia?

smart_16 %>% tabyl(comor)

 comor   n     percent valid_percent
     0 224 0.211920530   0.221782178
     1 315 0.298013245   0.311881188
     2 228 0.215704825   0.225742574
     3 130 0.122989593   0.128712871
     4  72 0.068117313   0.071287129
     5  29 0.027436140   0.028712871
     6   9 0.008514664   0.008910891
     7   3 0.002838221   0.002970297
    NA  47 0.044465468            NA

16.1.1 Any missing values?

We have 1057 observations (rows) in the smart_16 data set, of whom 860 have complete data on all variables.

dim(smart_16)

[1] 1057   10

n_case_complete(smart_16)

[1] 860

Which variables are missing?

miss_var_summary(smart_16)

# A tibble: 10 x 3
   variable   n_miss pct_miss
   <chr>       <int>    <dbl>
 1 activity       85    8.04 
 2 bmi            84    7.95 
 3 comor          47    4.45 
 4 smoke100       24    2.27 
 5 age_imp        12    1.14 
 6 hx_depress      3    0.284
 7 SEQNO           0    0    
 8 mmsa            0    0    
 9 physhealth      0    0    
10 bad_phys        0    0

Note that our outcomes (physhealth and the derived bad_phys) have no missing values here, by design. We will be performing multiple imputation to account appropriately for missingness in the predictors with missing values.

16.2 Obtaining a Simple Imputation with `mice`

The mice package provides several approaches we can use for imputation in building models of all kinds. Here, we’ll use it just to obtain a single set of imputed results that we can apply to “complete” our data for the purposes of thinking about (a) transforming our outcome and (b) considering the addition of non-linear predictor terms.

# requires library(mice)

set.seed(432)

# create small data set including only variables to
# be used in building the imputation model

sm16 <- smart_16 %>% 
    select(physhealth, activity, age_imp, bmi, comor, 
           hx_depress, smoke100)

smart_16_mice1 <- mice(sm16, m = 1)


 iter imp variable
  1   1  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   1  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   1  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   1  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   1  activity  age_imp  bmi  comor  hx_depress  smoke100

smart_16_imp1 <- mice::complete(smart_16_mice1)

n_case_miss(smart_16_imp1)

[1] 0

And now we’ll use this completed smart_16_imp1 data set (the product of just a single imputation) to help us address the next two issues.

16.3 Linear Regression: Considering a Transformation of the Outcome

A plausible strategy here would be to try to identify an outcome transformation only after some accounting for missing predictor values, perhaps through a simple imputation approach. However, to keep things simple here, I’ll just use the complete cases in this section.

Recall that our outcome here, physhealth can take the value 0, and is thus not strictly positive.

mosaic::favstats(~ physhealth, data = smart_16_imp1)

 min Q1 median Q3 max     mean       sd    n missing
   0  0      2 20  30 9.227058 11.92676 1057       0

So, if we want to investigate a potential transformation with a Box-Cox plot, we’ll have to add a small value to each physhealth value. We’ll add 1, so that the range of potential values is now from 1-31.

# requires library(car)

smart_16_imp1 %$% 
    boxCox((physhealth + 1) ~ age_imp + comor + smoke100 + 
               hx_depress + bmi + activity)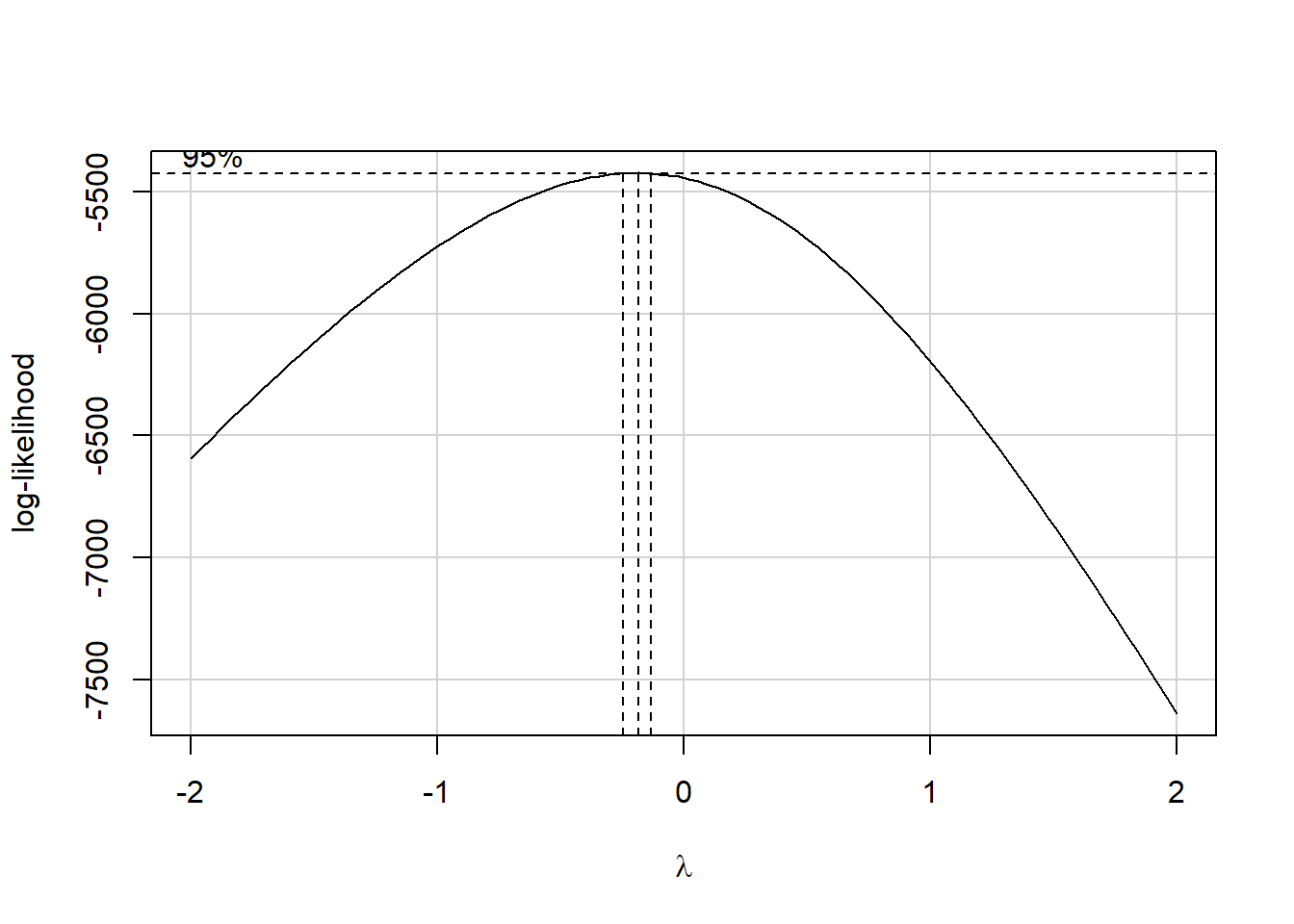

It looks like the logarithm is a reasonable transformation in this setting. So we’ll create a new outcome, that is the natural logarithm of (physhealth + 1), which we’ll call phys_tr to remind us that a transformation is involved that we’ll eventually need to back out of to make predictions. We’ll build this new variable in both our original smart_16 data set and in the simply imputed data set we’re using for just these early stages.

smart_16_imp1 <- smart_16_imp1 %>%
    mutate(phys_tr = log(physhealth + 1))

smart_16 <- smart_16 %>%
    mutate(phys_tr = log(physhealth + 1))

So we have phys_tr = log(physhealth + 1)

where we are referring above to the natural (base $e$ logarithm).

We can also specify our back-transformation to the original physhealth values from our new phys_tr as physhealth = exp(phys_tr) - 1.

16.4 Linear Regression: Considering Non-Linearity in the Predictors

Consider the following Spearman $\rho^2$ plot.

# requires rms package 
# (technically Hmisc, which is loaded by rms)

smart_16_imp1 %$% 
    plot(spearman2(phys_tr ~ age_imp + comor + smoke100 + 
           hx_depress + bmi + activity))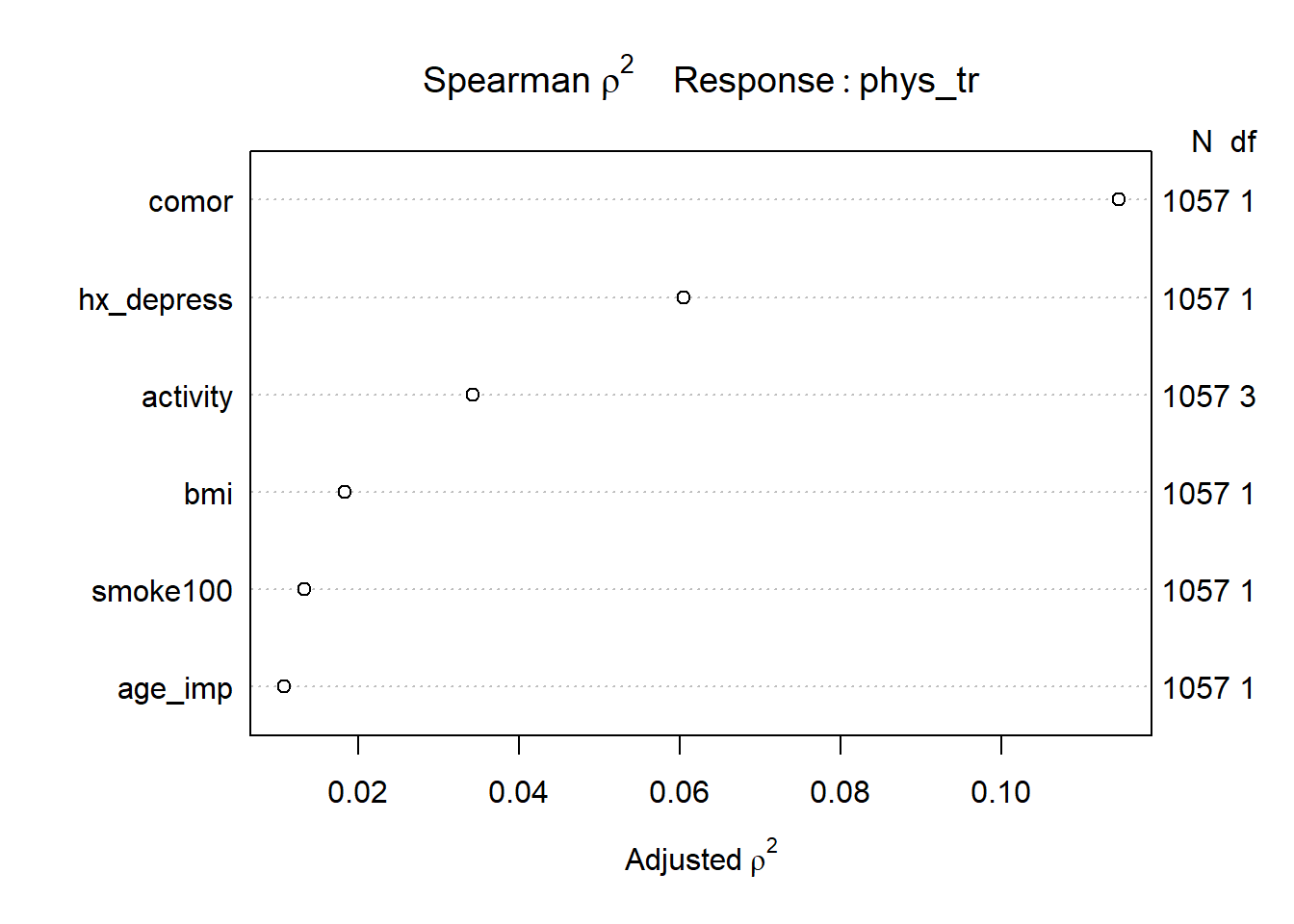

After our single imputation, we have the same N value in all rows of this plot, which is what we want to see. It appears that in considering potential non-linear terms, comor and hx_depress and perhaps activity are worthy of increased attention. I’ll make a couple of arbitrary choices, to add a raw cubic polynomial to represent the comor information, and we’ll add an interaction term between hx_depress and activity.

16.5 “Main Effects” Linear Regression with `lm` on the Complete Cases

Recall that we have 860 complete cases in our smart_16 data, out of a total of 1057 observations in total. A model using only the complete cases should thus drop the remaining 197 subjects. Let’s see if a main effects only model for our newly transformed phys_tr outcome does in fact do this.

m_1cc <- smart_16 %$% 
    lm(phys_tr ~ age_imp + comor + smoke100 + 
           hx_depress + bmi + activity)

summary(m_1cc)


Call:
lm(formula = phys_tr ~ age_imp + comor + smoke100 + hx_depress + 
    bmi + activity)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.0802 -1.0399 -0.2917  1.1032  2.8479 

Coefficients:
                               Estimate Std. Error t value Pr(>|t|)    
(Intercept)                    0.582257   0.370909   1.570   0.1168    
age_imp                       -0.007044   0.003813  -1.847   0.0651 .  
comor                          0.301805   0.033104   9.117  < 2e-16 ***
smoke100                       0.099032   0.090281   1.097   0.2730    
hx_depress                     0.471915   0.104232   4.528 6.82e-06 ***
bmi                            0.016364   0.006295   2.599   0.0095 ** 
activityActive                -0.229865   0.154912  -1.484   0.1382    
activityInsufficiently_Active -0.116912   0.139439  -0.838   0.4020    
activityInactive               0.256188   0.115265   2.223   0.0265 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.303 on 851 degrees of freedom
  (197 observations deleted due to missingness)
Multiple R-squared:  0.1806,    Adjusted R-squared:  0.1729 
F-statistic: 23.45 on 8 and 851 DF,  p-value: < 2.2e-16

Note that the appropriate number of observations are listed as “deleted due to missingness.”

16.5.1 Quality of Fit Statistics

glance(m_1cc) %>%
    select(r.squared, adj.r.squared, sigma, AIC, BIC) %>%
    kable(digits = c(3, 3, 2, 1, 1))

r.squared	adj.r.squared	sigma	AIC	BIC
0.181	0.173	1.3	2906.3	2953.9

16.5.2 Interpreting Effect Sizes

tidy(m_1cc, conf.int = TRUE) %>%
    select(term, estimate, std.error, conf.low, conf.high) %>%
    kable(digits = 3)

term	estimate	std.error	conf.low	conf.high
(Intercept)	0.582	0.371	-0.146	1.310
age_imp	-0.007	0.004	-0.015	0.000
comor	0.302	0.033	0.237	0.367
smoke100	0.099	0.090	-0.078	0.276
hx_depress	0.472	0.104	0.267	0.676
bmi	0.016	0.006	0.004	0.029
activityActive	-0.230	0.155	-0.534	0.074
activityInsufficiently_Active	-0.117	0.139	-0.391	0.157
activityInactive	0.256	0.115	0.030	0.482

We’ll interpret three of the predictors here to demonstrate ideas: comor, hx_depress and activity.

If we have two subjects with the same values of age_imp, smoke100, hx_depress, bmi, and activity, but Harry has a comor score that is one point higher than Sally’s, then the model predicts that Harry’s transformed outcome (specifically the natural logarithm of (his physhealth days + 1)) will be 0.302 higher than Sally’s, with a 95% confidence interval around that estimate ranging from (round(a$conf.low,3), round(a$conf.high,3)).
If we have two subjects with the same values of age_imp, comor, smoke100, bmi, and activity, but Harry has a history of depression (hx_depress = 1) while Sally does not have such a history (so Sally’s hx_depress = 0), then the model predicts that Harry’s transformed outcome (specifically the natural logarithm of (his physhealth days + 1)) will be 0.472 higher than Sally’s, with a 95% confidence interval around that estimate ranging from (round(a$conf.low,3), round(a$conf.high,3)).
The activity variable has four categories as indicated in the table below. The model uses the “Highly_Active” category as the reference group.

smart_16_imp1 %>% tabyl(activity)

              activity   n   percent
         Highly_Active 240 0.2270577
                Active 138 0.1305582
 Insufficiently_Active 193 0.1825922
              Inactive 486 0.4597919

From the tidied set of coefficients, we can describe the activity effects as follows.
- If Sally is “Highly Active” and Harry is “Active” but they otherwise have the same values of all predictors, then our prediction is that Harry’s transformed outcome (specifically the natural logarithm of (his physhealth days + 1)) will be 0.23 lower than Sally’s, with a 95% confidence interval around that estimate ranging from (round(a$conf.low,3), round(a$conf.high,3)).
- If instead Harry is “Insufficiently Active” but nothing else changes, then our prediction is that Harry’s transformed outcome will be 0.117 lower than Sally’s, with a 95% confidence interval around that estimate ranging from (round(a2$conf.low,3), round(a2$conf.high,3)).
- If instead Harry is “Inactive” but nothing else changes, then our prediction is that Harry’s transformed outcome will be -0.117 higher than Sally’s, with a 95% confidence interval around that estimate ranging from (round(a2$conf.low,3), round(a2$conf.high,3)).

16.5.3 Making Predictions with the Model

Let’s describe two subjects, and use this model (and the ones that follow) to predict their physhealth values.

Sheena is age 50, has 2 comorbidities, has smoked 100 cigarettes in her life, has no history of depression, a BMI of 25, and is Highly Active.
Jacob is age 65, has 4 comorbidities, has never smoked, has a history of depression, a BMI of 32 and is Inactive.

We’ll first build predictions for Sheena and Jacob (with 95% prediction intervals) for phys_tr.

new2 <- tibble(
    name = c("Sheena", "Jacob"),
    age_imp = c(50, 65),
    comor = c(2, 4),
    smoke100 = c(1, 0),
    hx_depress = c(0, 1),
    bmi = c(25, 32),
    activity = c("Highly_Active", "Inactive")
)

preds_m_1cc <- predict(m_1cc, newdata = new2, 
                       interval = "prediction")

preds_m_1cc

       fit         lwr      upr
1 1.341780 -1.22938687 3.912946
2 2.583342  0.01398071 5.152704

The model makes predictions for our transformed outcome, phys_tr. Now, we need to back-transform the predictions and the confidence intervals to build predictions for physhealth.

preds_m_1cc <- preds_m_1cc %>%
    tbl_df() %>%
    mutate(names = c("Sheena", "Jacob"),
           pred_physhealth = exp(fit) - 1,
           conf_low = exp(lwr) - 1,
           conf_high = exp(upr) - 1) %>%
    select(names, pred_physhealth, conf_low, conf_high, 
           everything())

preds_m_1cc %>% kable(digits = 3)

names	pred_physhealth	conf_low	conf_high	fit	lwr	upr
Sheena	2.826	-0.708	49.046	1.342	-1.229	3.913
Jacob	12.241	0.014	171.898	2.583	0.014	5.153

16.6 “Augmented” Linear Regression with `lm` on the Complete Cases

Now, we’ll add the non-linear terms we discussed earlier. We’ll add a (raw) cubic polynomial to represent the comor information, and we’ll add an interaction term between hx_depress and activity.

# requires rms package (and co-loading Hmisc)

m_2cc <- smart_16 %$% 
    lm(phys_tr ~ age_imp + pol(comor, 3) + smoke100 + 
           bmi + hx_depress*activity)

summary(m_2cc)


Call:
lm(formula = phys_tr ~ age_imp + pol(comor, 3) + smoke100 + bmi + 
    hx_depress * activity)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.9073 -1.0627 -0.2669  1.1429  2.9240 

Coefficients:
                                          Estimate Std. Error t value Pr(>|t|)
(Intercept)                               0.515147   0.376262   1.369  0.17133
age_imp                                  -0.008102   0.003865  -2.096  0.03637
pol(comor, 3)comor                        0.634293   0.160632   3.949 8.51e-05
pol(comor, 3)comor^2                     -0.130619   0.073526  -1.776  0.07601
pol(comor, 3)comor^3                      0.012507   0.008977   1.393  0.16390
smoke100                                  0.089338   0.090337   0.989  0.32297
bmi                                       0.015192   0.006315   2.406  0.01636
hx_depress                                0.647035   0.229698   2.817  0.00496
activityActive                           -0.202152   0.172301  -1.173  0.24102
activityInsufficiently_Active            -0.005705   0.166219  -0.034  0.97263
activityInactive                          0.290450   0.132197   2.197  0.02828
hx_depress:activityActive                -0.124742   0.395417  -0.315  0.75248
hx_depress:activityInsufficiently_Active -0.376438   0.310162  -1.214  0.22521
hx_depress:activityInactive              -0.172960   0.267428  -0.647  0.51797
                                            
(Intercept)                                 
age_imp                                  *  
pol(comor, 3)comor                       ***
pol(comor, 3)comor^2                     .  
pol(comor, 3)comor^3                        
smoke100                                    
bmi                                      *  
hx_depress                               ** 
activityActive                              
activityInsufficiently_Active               
activityInactive                         *  
hx_depress:activityActive                   
hx_depress:activityInsufficiently_Active    
hx_depress:activityInactive                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.301 on 846 degrees of freedom
  (197 observations deleted due to missingness)
Multiple R-squared:  0.187, Adjusted R-squared:  0.1745 
F-statistic: 14.97 on 13 and 846 DF,  p-value: < 2.2e-16

Note again that the appropriate number of observations are listed as “deleted due to missingness.”

16.6.1 Quality of Fit Statistics

glance(m_2cc) %>%
    select(r.squared, adj.r.squared, sigma, AIC, BIC) %>%
    kable(digits = c(3, 3, 2, 1, 1))

r.squared	adj.r.squared	sigma	AIC	BIC
0.187	0.175	1.3	2909.6	2980.9

16.6.2 ANOVA assessing the impact of the non-linear terms

anova(m_1cc, m_2cc)

Analysis of Variance Table

Model 1: phys_tr ~ age_imp + comor + smoke100 + hx_depress + bmi + activity
Model 2: phys_tr ~ age_imp + pol(comor, 3) + smoke100 + bmi + hx_depress * 
    activity
  Res.Df    RSS Df Sum of Sq      F Pr(>F)
1    851 1444.0                           
2    846 1432.8  5    11.266 1.3304  0.249

The difference between the models doesn’t meet the standard for statistical detectabilty at our usual $\alpha$ levels.

16.6.3 Interpreting Effect Sizes

tidy(m_2cc, conf.int = TRUE) %>%
    select(term, estimate, std.error, conf.low, conf.high) %>%
    kable(digits = 3)

term	estimate	std.error	conf.low	conf.high
(Intercept)	0.515	0.376	-0.223	1.254
age_imp	-0.008	0.004	-0.016	-0.001
pol(comor, 3)comor	0.634	0.161	0.319	0.950
pol(comor, 3)comor^2	-0.131	0.074	-0.275	0.014
pol(comor, 3)comor^3	0.013	0.009	-0.005	0.030
smoke100	0.089	0.090	-0.088	0.267
bmi	0.015	0.006	0.003	0.028
hx_depress	0.647	0.230	0.196	1.098
activityActive	-0.202	0.172	-0.540	0.136
activityInsufficiently_Active	-0.006	0.166	-0.332	0.321
activityInactive	0.290	0.132	0.031	0.550
hx_depress:activityActive	-0.125	0.395	-0.901	0.651
hx_depress:activityInsufficiently_Active	-0.376	0.310	-0.985	0.232
hx_depress:activityInactive	-0.173	0.267	-0.698	0.352

Let’s focus first on interpreting the interaction terms between hx_depress and activity.

Assume first that we have a set of subjects with the same values of age_imp, smoke100, bmi, and comor.

Arnold has hx_depress = 1 and is Inactive
Betty has hx_depress = 1 and is Insufficiently Active
Carlos has hx_depress = 1 and is Active
Debbie has hx_depress = 1 and is Highly Active
Eamon has hx_depress = 0 and is Inactive
Florence has hx_depress = 0 and is Insufficiently Active
Garry has hx_depress = 0 and is Active
Harry has hx_depress = 0 and is Highly Active

So the model, essentially can be used to compare each of the first seven people on that list to Harry (who has the reference levels of both hx_depress and activity.) Let’s compare Arnold to Harry.

For instance, as compared to Harry, Arnold is expected to have a transformed outcome (specifically the natural logarithm of (his physhealth days + 1)) that is:

0.647 higher because Arnold’s hx_depress = 1, and
0.29 higher still because Arnold’s activity is “Inactive”, and
0.173 lower because of the combination (see the `hx_depress:activityInactive" row)

So, in total, we expect Arnold’s transformed outcome to be 0.647 + 0.29 + (-0.173), or 0.764 higher than Harry’s.

If we want to compare Arnold to, for instance, Betty, we first calculate Betty’s difference from Harry, and then compare the two differences.

As compared to Harry, Betty is expected to have a transformed outcome (specifically the natural logarithm of (her physhealth days + 1)) that is:

0.647 higher because Betty’s hx_depress = 1, and
0.006 lower still because Betty’s activity is “Insufficiently Active”, and
0.376 lower because of the combination (see the `hx_depress:activityInsufficiently_Active" row)

So, in total, we expect Betty’s transformed outcome to be 0.647 + (-0.006) + (-0.376), or 0.265 higher than Harry’s.

And thus we can compare Betty and Arnold directly.

Arnold is predicted to have an outcome that is 0.764 higher than Harry’s.
Betty is predicted to have an outcome that is 0.265 higher than Harry’s.
And so Arnold’s predicted outcome (phys_tr) is 0.499 larger than Betty’s.

Now, suppose we want to look at our cubic polynomial in comor.

Suppose Harry and Sally have the same values for all other predictors in the model, but Harry has 1 comorbidity where Sally has none. Then the three terms in the model related to comor will be 1 for Harry and 0 for Sally, and the interpretation becomes pretty straightforward.
But suppose instead that nothing has changed except Harry has 2 comorbidities and Sally has just 1. The size of the impact of this Harry - Sally difference is far larger in this situation, because the comor variable enters the model in a non-linear way. This is an area where fitting the model using ols can be helpful because of the ability to generate plots (of effects, nomograms, etc.) that can show this non-linearity in a clear way.

Suppose for instance, that Harry and Sally share the following values for the other predictors: each is age 40, has never smoked, has no history of depression, a BMI of 30 and is Highly Active.

Now, if Harry has 1 comorbidity and Sally has none, the predicted phys_tr values for Harry and Sally are as indicated below.

hands1 <- tibble(
    name = c("Harry", "Sally"),
    age_imp = c(40, 40),
    comor = c(1, 0),
    smoke100 = c(0, 0),
    hx_depress = c(0, 0),
    bmi = c(30, 30),
    activity = c("Highly_Active", "Highly_Active")
)

predict(m_2cc, newdata = hands1)

        1         2 
1.1630262 0.6468457

But if Harry has 2 comorbidities and Sally 1, the predictions are:

hands2 <- tibble(
    name = c("Harry", "Sally"),
    age_imp = c(40, 40),
    comor = c(2, 1), # only thing that changes
    smoke100 = c(0, 0),
    hx_depress = c(0, 0),
    bmi = c(30, 30),
    activity = c("Highly_Active", "Highly_Active")
)

predict(m_2cc, newdata = hands2)

       1        2 
1.493011 1.163026

Note that the difference in predictions between Harry and Sally is much smaller now than it was previously.

16.6.4 Making Predictions with the Model

As before, we’ll use the new model to predict physhealth values for Sheena and Jacob.

Sheena is age 50, has 2 comorbidities, has smoked 100 cigarettes in her life, has no history of depression, a BMI of 25, and is Highly Active.
Jacob is age 65, has 4 comorbidities, has never smoked, has a history of depression, a BMI of 32 and is Inactive.

We’ll first build predictions for Sheena and Jacob (with 95% prediction intervals) for phys_tr.

new2 <- tibble(
    name = c("Sheena", "Jacob"),
    age_imp = c(50, 65),
    comor = c(2, 4),
    smoke100 = c(1, 0),
    hx_depress = c(0, 1),
    bmi = c(25, 32),
    activity = c("Highly_Active", "Inactive")
)

preds_m_2cc <- predict(m_2cc, newdata = new2, 
                       interval = "prediction")

preds_m_2cc

       fit        lwr      upr
1 1.425371 -1.1470863 3.997828
2 2.486928 -0.0863505 5.060207

Now, we need to back-transform the predictions and the confidence intervals that describe phys_tr to build predictions for physhealth.

preds_m_2cc <- preds_m_2cc %>%
    tbl_df() %>%
    mutate(names = c("Sheena", "Jacob"),
           pred_physhealth = exp(fit) - 1,
           conf_low = exp(lwr) - 1,
           conf_high = exp(upr) - 1) %>%
    select(names, pred_physhealth, conf_low, conf_high, 
           everything())

preds_m_2cc %>% kable(digits = 3)

names	pred_physhealth	conf_low	conf_high	fit	lwr	upr
Sheena	3.159	-0.682	53.480	1.425	-1.147	3.998
Jacob	11.024	-0.083	156.623	2.487	-0.086	5.060

16.7 Using `mice` to perform Multiple Imputation

Let’s focus on the main effects model, and look at the impact of performing multiple imputation to account for the missing data. Recall that in our smart_16 data, the most “missingness” is shown in the activity variable, which is still missing less than 10% of the time. So we’ll try a set of 10 imputations, using the default settings in the mice package.

# requires library(mice)

set.seed(432)

# create small data set including only variables to
# be used in building the imputation model

sm16 <- smart_16 %>% 
    select(physhealth, phys_tr, activity, age_imp, bmi, comor, 
           hx_depress, smoke100)

smart_16_mice10 <- mice(sm16, m = 10)


 iter imp variable
  1   1  activity  age_imp  bmi  comor  hx_depress  smoke100
  1   2  activity  age_imp  bmi  comor  hx_depress  smoke100
  1   3  activity  age_imp  bmi  comor  hx_depress  smoke100
  1   4  activity  age_imp  bmi  comor  hx_depress  smoke100
  1   5  activity  age_imp  bmi  comor  hx_depress  smoke100
  1   6  activity  age_imp  bmi  comor  hx_depress  smoke100
  1   7  activity  age_imp  bmi  comor  hx_depress  smoke100
  1   8  activity  age_imp  bmi  comor  hx_depress  smoke100
  1   9  activity  age_imp  bmi  comor  hx_depress  smoke100
  1   10  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   1  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   2  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   3  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   4  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   5  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   6  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   7  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   8  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   9  activity  age_imp  bmi  comor  hx_depress  smoke100
  2   10  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   1  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   2  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   3  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   4  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   5  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   6  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   7  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   8  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   9  activity  age_imp  bmi  comor  hx_depress  smoke100
  3   10  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   1  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   2  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   3  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   4  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   5  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   6  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   7  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   8  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   9  activity  age_imp  bmi  comor  hx_depress  smoke100
  4   10  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   1  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   2  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   3  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   4  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   5  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   6  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   7  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   8  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   9  activity  age_imp  bmi  comor  hx_depress  smoke100
  5   10  activity  age_imp  bmi  comor  hx_depress  smoke100

summary(smart_16_mice10)

Class: mids
Number of multiple imputations:  10 
Imputation methods:
physhealth    phys_tr   activity    age_imp        bmi      comor hx_depress 
        ""         ""  "polyreg"      "pmm"      "pmm"      "pmm"      "pmm" 
  smoke100 
     "pmm" 
PredictorMatrix:
           physhealth phys_tr activity age_imp bmi comor hx_depress smoke100
physhealth          0       1        1       1   1     1          1        1
phys_tr             1       0        1       1   1     1          1        1
activity            1       1        0       1   1     1          1        1
age_imp             1       1        1       0   1     1          1        1
bmi                 1       1        1       1   0     1          1        1
comor               1       1        1       1   1     0          1        1

16.8 Running the Linear Regression in `lm` with Multiple Imputation

Next, we’ll run the linear model (main effects) on each of the 10 imputed data sets.

m10_mods <- 
    with(smart_16_mice10, lm(phys_tr ~ age_imp + comor + 
                                 smoke100 + hx_depress + 
                                 bmi + activity))

summary(m10_mods)

# A tibble: 90 x 5
   term                          estimate std.error statistic  p.value
   <chr>                            <dbl>     <dbl>     <dbl>    <dbl>
 1 (Intercept)                    0.518     0.330       1.57  1.17e- 1
 2 age_imp                       -0.00563   0.00338    -1.66  9.64e- 2
 3 comor                          0.305     0.0295     10.3   5.77e-24
 4 smoke100                       0.123     0.0806      1.53  1.28e- 1
 5 hx_depress                     0.490     0.0939      5.22  2.13e- 7
 6 bmi                            0.0145    0.00564     2.57  1.03e- 2
 7 activityActive                -0.200     0.137      -1.46  1.45e- 1
 8 activityInsufficiently_Active -0.0298    0.126      -0.236 8.13e- 1
 9 activityInactive               0.251     0.105       2.40  1.65e- 2
10 (Intercept)                    0.429     0.328       1.31  1.91e- 1
# ... with 80 more rows

Then, we’ll pool results across the 10 imputations

m10_pool <- pool(m10_mods)
summary(m10_pool, conf.int = TRUE) %>%
    select(-statistic, -df) %>%
    kable(digits = 3)

term	estimate	std.error	p.value	2.5 %	97.5 %
(Intercept)	0.482	0.338	0.154	-0.181	1.146
age_imp	-0.005	0.003	0.116	-0.012	0.001
comor	0.308	0.030	0.000	0.249	0.367
smoke100	0.106	0.081	0.193	-0.054	0.266
hx_depress	0.511	0.094	0.000	0.327	0.695
bmi	0.015	0.006	0.011	0.003	0.026
activityActive	-0.206	0.145	0.157	-0.490	0.079
activityInsufficiently_Active	-0.047	0.127	0.710	-0.297	0.203
activityInactive	0.264	0.106	0.014	0.055	0.473

And we can compare these results to the complete case analysis we completed earlier.

tidy(m_1cc, conf.int = TRUE) %>%
    select(term, estimate, std.error, p.value, conf.low, conf.high) %>%
    kable(digits = 3)

term	estimate	std.error	p.value	conf.low	conf.high
(Intercept)	0.582	0.371	0.117	-0.146	1.310
age_imp	-0.007	0.004	0.065	-0.015	0.000
comor	0.302	0.033	0.000	0.237	0.367
smoke100	0.099	0.090	0.273	-0.078	0.276
hx_depress	0.472	0.104	0.000	0.267	0.676
bmi	0.016	0.006	0.010	0.004	0.029
activityActive	-0.230	0.155	0.138	-0.534	0.074
activityInsufficiently_Active	-0.117	0.139	0.402	-0.391	0.157
activityInactive	0.256	0.115	0.027	0.030	0.482

Note that there are some sizeable differences here, although nothing enormous.

If we want the pooled $R^2$ or pooled adjusted $R^2$ after imputation, R will provide it (and a 95% confidence interval around the estimate) with …

pool.r.squared(m10_mods)

          est     lo 95    hi 95 fmi
R^2 0.1890102 0.1475229 0.233104 NaN

pool.r.squared(m10_mods, adjusted = TRUE)

             est     lo 95     hi 95 fmi
adj R^2 0.182819 0.1417737 0.2266046 NaN

We can see the fraction of missing information about each coefficient due to non-response (fmi) and other details with the following code…

m10_pool

Class: mipo    m = 10 
                           term  m     estimate         ubar            b
1                   (Intercept) 10  0.482435070 1.094155e-01 4.462766e-03
2                       age_imp 10 -0.005349353 1.136427e-05 1.940740e-07
3                         comor 10  0.308124658 8.856752e-04 2.082107e-05
4                      smoke100 10  0.105918127 6.497097e-03 1.124020e-04
5                    hx_depress 10  0.511204803 8.714280e-03 8.952294e-05
6                           bmi 10  0.014957236 3.217217e-05 2.054686e-06
7                activityActive 10 -0.205549126 1.927714e-02 1.559248e-03
8 activityInsufficiently_Active 10 -0.047380210 1.580064e-02 3.874612e-04
9              activityInactive 10  0.263506880 1.068536e-02 5.884273e-04
             t dfcom        df        riv     lambda        fmi
1 1.143246e-01  1048  830.7183 0.04486606 0.04293953 0.04523541
2 1.157775e-05  1048  988.3826 0.01878532 0.01843894 0.02041912
3 9.085784e-04  1048  951.1643 0.02585957 0.02520771 0.02725094
4 6.620740e-03  1048  987.2042 0.01903038 0.01867499 0.02065706
5 8.812756e-03  1048 1019.6853 0.01130044 0.01117417 0.01310795
6 3.443232e-05  1048  665.8138 0.07025186 0.06564049 0.06843457
7 2.099231e-02  1048  560.9089 0.08897444 0.08170480 0.08496170
8 1.622685e-02  1048  944.7700 0.02697405 0.02626556 0.02832035
9 1.133263e-02  1048  726.5358 0.06057541 0.05711561 0.05970050

16.9 Fit the Multiple Imputation Model with `aregImpute`

Here, we’ll use aregImpute to deal with missing values through multiple imputation, and use the ols function in the rms package to fit the model.

The first step is to fit the multiple imputation model. We’ll use n.impute = 10 imputations, with B = 10 bootstrap samples for the preditive mean matching, and fit both linear models and models with restricted cubic splines with 3 knots (nk = c(0, 3)) allowing the target variable to have a non-linear transformation when nk is 3, via tlinear = FALSE.

set.seed(43201602)
dd <- datadist(smart_16)
options(datadist = "dd")

fit16_imp <- 
    aregImpute(~ phys_tr + age_imp + comor + smoke100 + 
                   hx_depress + bmi + activity,
               nk = c(0, 3), tlinear = FALSE, 
               data = smart_16, B = 10, n.impute = 10)

Iteration 1 
Iteration 2 
Iteration 3 
Iteration 4 
Iteration 5 
Iteration 6 
Iteration 7 
Iteration 8 
Iteration 9 
Iteration 10 
Iteration 11 
Iteration 12 
Iteration 13

Here are the results of that imputation model.

fit16_imp


Multiple Imputation using Bootstrap and PMM

aregImpute(formula = ~phys_tr + age_imp + comor + smoke100 + 
    hx_depress + bmi + activity, data = smart_16, n.impute = 10, 
    nk = c(0, 3), tlinear = FALSE, B = 10)

n: 1057     p: 7    Imputations: 10     nk: 0 

Number of NAs:
   phys_tr    age_imp      comor   smoke100 hx_depress        bmi   activity 
         0         12         47         24          3         84         85 

           type d.f.
phys_tr       s    1
age_imp       s    1
comor         s    1
smoke100      l    1
hx_depress    l    1
bmi           s    1
activity      c    3

R-squares for Predicting Non-Missing Values for Each Variable
Using Last Imputations of Predictors
   age_imp      comor   smoke100 hx_depress        bmi   activity 
     0.212      0.202      0.056      0.166      0.173      0.058 

Resampling results for determining the complexity of imputation models

Variable being imputed: age_imp 
                                          nk=0   nk=3
Bootstrap bias-corrected R^2             0.183  0.209
10-fold cross-validated  R^2             0.209  0.213
Bootstrap bias-corrected mean   |error|  9.151 11.026
10-fold cross-validated  mean   |error| 65.128 11.054
Bootstrap bias-corrected median |error|  7.388  8.734
10-fold cross-validated  median |error| 65.936  8.775

Variable being imputed: comor 
                                         nk=0  nk=3
Bootstrap bias-corrected R^2            0.172 0.175
10-fold cross-validated  R^2            0.177 0.186
Bootstrap bias-corrected mean   |error| 0.989 1.209
10-fold cross-validated  mean   |error| 1.748 1.194
Bootstrap bias-corrected median |error| 0.835 0.928
10-fold cross-validated  median |error| 1.539 0.906

Variable being imputed: smoke100 
                                          nk=0   nk=3
Bootstrap bias-corrected R^2            0.0179 0.0138
10-fold cross-validated  R^2            0.0321 0.0179
Bootstrap bias-corrected mean   |error| 0.4876 0.4891
10-fold cross-validated  mean   |error| 0.9549 0.9653
Bootstrap bias-corrected median |error| 0.4833 0.4827
10-fold cross-validated  median |error| 0.8735 0.8771

Variable being imputed: hx_depress 
                                         nk=0  nk=3
Bootstrap bias-corrected R^2            0.156 0.138
10-fold cross-validated  R^2            0.147 0.148
Bootstrap bias-corrected mean   |error| 0.356 0.361
10-fold cross-validated  mean   |error| 0.804 0.788
Bootstrap bias-corrected median |error| 0.333 0.339
10-fold cross-validated  median |error| 0.716 0.681

Variable being imputed: bmi 
                                          nk=0  nk=3
Bootstrap bias-corrected R^2             0.120 0.122
10-fold cross-validated  R^2             0.133 0.138
Bootstrap bias-corrected mean   |error|  5.305 6.858
10-fold cross-validated  mean   |error| 32.527 6.932
Bootstrap bias-corrected median |error|  4.198 5.768
10-fold cross-validated  median |error| 31.458 5.861

Variable being imputed: activity 
                                          nk=0   nk=3
Bootstrap bias-corrected R^2            0.0310 0.0259
10-fold cross-validated  R^2            0.0426 0.0362
Bootstrap bias-corrected mean   |error| 1.9044 1.9150
10-fold cross-validated  mean   |error| 1.0801 1.0783
Bootstrap bias-corrected median |error| 2.0000 2.0000
10-fold cross-validated  median |error| 1.0000 1.0000

par(mfrow = c(3,2))
plot(fit16_imp)

par(mfrow = c(1,1))

The plot helps us see where the imputations are happening.

16.10 Fit Linear Regression using `ols` and `fit.mult.impute`

m16_imp <- 
    fit.mult.impute(phys_tr ~ age_imp + comor + smoke100 +
                        hx_depress + bmi + activity,
                    fitter = ols, xtrans = fit16_imp,
                    data = smart_16, x = TRUE, y = TRUE)


Variance Inflation Factors Due to Imputation:

                     Intercept                        age_imp 
                          1.02                           1.03 
                         comor                       smoke100 
                          1.05                           1.03 
                    hx_depress                            bmi 
                          1.04                           1.06 
               activity=Active activity=Insufficiently_Active 
                          1.10                           1.08 
             activity=Inactive 
                          1.13 

Rate of Missing Information:

                     Intercept                        age_imp 
                          0.02                           0.03 
                         comor                       smoke100 
                          0.05                           0.03 
                    hx_depress                            bmi 
                          0.04                           0.06 
               activity=Active activity=Insufficiently_Active 
                          0.09                           0.07 
             activity=Inactive 
                          0.12 

d.f. for t-distribution for Tests of Single Coefficients:

                     Intercept                        age_imp 
                      17027.11                       13861.68 
                         comor                       smoke100 
                       4117.52                       10238.67 
                    hx_depress                            bmi 
                       5689.23                        2750.04 
               activity=Active activity=Insufficiently_Active 
                       1122.57                        1771.45 
             activity=Inactive 
                        679.79 

The following fit components were averaged over the 10 model fits:

  fitted.values stats linear.predictors

16.10.1 Summaries and Coefficients

Here are the results:

m16_imp

Linear Regression Model
 
 fit.mult.impute(formula = phys_tr ~ age_imp + comor + smoke100 + 
     hx_depress + bmi + activity, fitter = ols, xtrans = fit16_imp, 
     data = smart_16, x = TRUE, y = TRUE)
 
                Model Likelihood     Discrimination    
                   Ratio Test           Indexes        
 Obs    1057    LR chi2    221.70    R2       0.189    
 sigma1.2870    d.f.            8    R2 adj   0.183    
 d.f.   1048    Pr(> chi2) 0.0000    g        0.689    
 
 Residuals
 
     Min      1Q  Median      3Q     Max 
 -3.1262 -1.0221 -0.2857  1.0879  2.8277 
 
 
                                Coef    S.E.   t     Pr(>|t|)
 Intercept                       0.4209 0.3336  1.26 0.2074  
 age_imp                        -0.0051 0.0034 -1.50 0.1332  
 comor                           0.3098 0.0303 10.21 <0.0001 
 smoke100                        0.1096 0.0817  1.34 0.1800  
 hx_depress                      0.5150 0.0951  5.42 <0.0001 
 bmi                             0.0163 0.0058  2.79 0.0053  
 activity=Active                -0.1772 0.1455 -1.22 0.2237  
 activity=Insufficiently_Active -0.0430 0.1298 -0.33 0.7404  
 activity=Inactive               0.2479 0.1097  2.26 0.0241

16.10.2 Effect Sizes

We can plot and summarize the effect sizes using the usual ols tools:

summary(m16_imp)

             Effects              Response : phys_tr 

 Factor                                    Low   High  Diff. Effect    S.E.    
 age_imp                                   57.00 73.00 16.00 -0.081824 0.054450
 comor                                      1.00  2.00  1.00  0.309760 0.030341
 smoke100                                   0.00  1.00  1.00  0.109590 0.081678
 hx_depress                                 0.00  1.00  1.00  0.515010 0.095071
 bmi                                       27.29 36.65  9.36  0.152300 0.054517
 activity - Highly_Active:Inactive          4.00  1.00    NA -0.247890 0.109730
 activity - Active:Inactive                 4.00  2.00    NA -0.425090 0.138280
 activity - Insufficiently_Active:Inactive  4.00  3.00    NA -0.290930 0.112040
 Lower 0.95 Upper 0.95
 -0.188670   0.025019 
  0.250220   0.369290 
 -0.050680   0.269860 
  0.328460   0.701560 
  0.045324   0.259270 
 -0.463210  -0.032569 
 -0.696420  -0.153760 
 -0.510770  -0.071083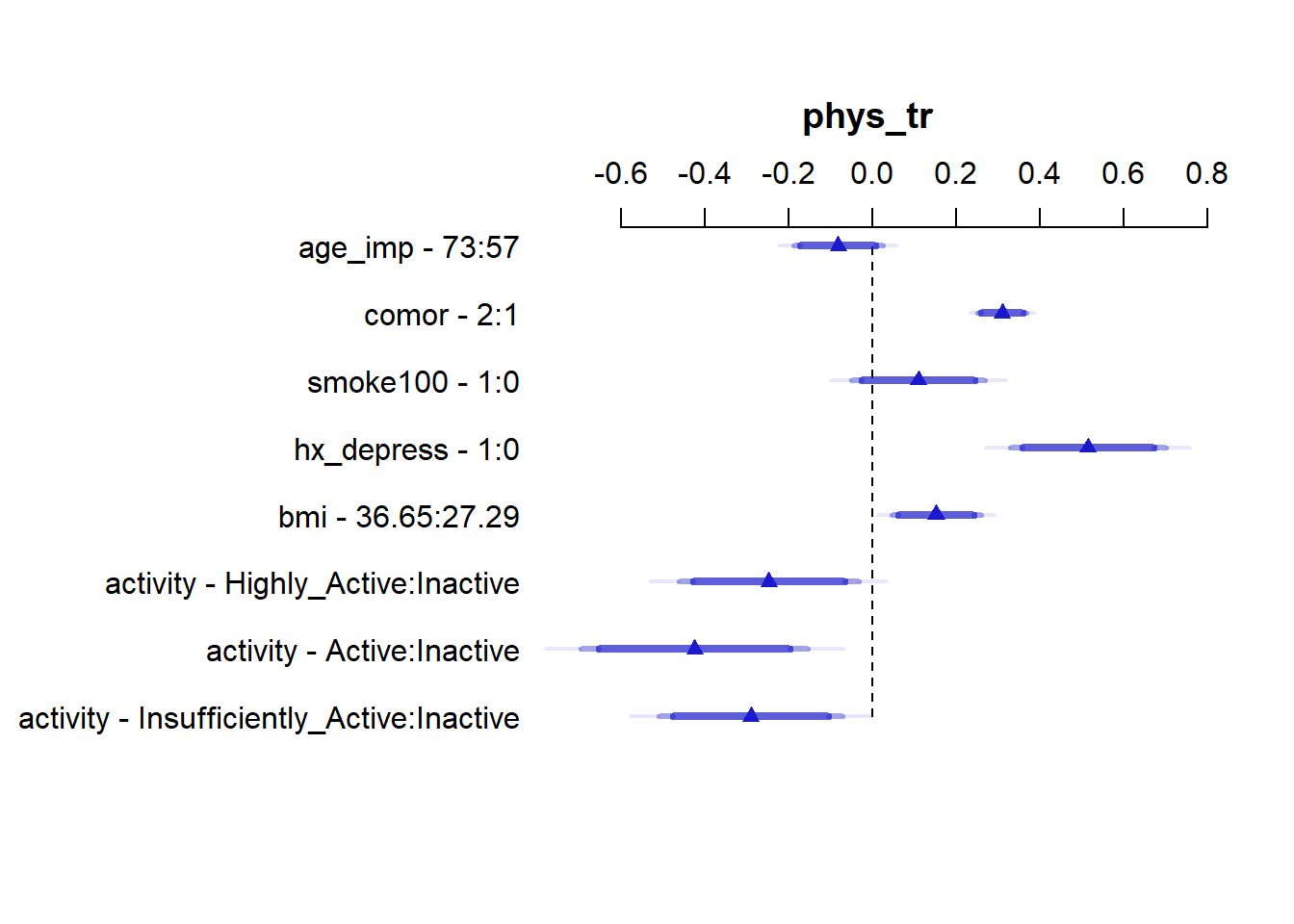

plot(summary(m16_imp))

16.10.3 Making Predictions with this Model

Once again, let’s make predictions for our two subjects, and use this model (and the ones that follow) to predict their physhealth values.

Sheena is age 50, has 2 comorbidities, has smoked 100 cigarettes in her life, has no history of depression, a BMI of 25, and is Highly Active.
Jacob is age 65, has 4 comorbidities, has never smoked, has a history of depression, a BMI of 32 and is Inactive.

new2 <- tibble(
    name = c("Sheena", "Jacob"),
    age_imp = c(50, 65),
    comor = c(2, 4),
    smoke100 = c(1, 0),
    hx_depress = c(0, 1),
    bmi = c(25, 32),
    activity = c("Highly_Active", "Inactive")
)

preds_m_16imp <- predict(m16_imp, 
                         newdata = data.frame(new2))

preds_m_16imp

       1        2 
1.301066 2.611073

preds_m_16imp <- preds_m_16imp %>%
    tbl_df() %>%
    mutate(names = c("Sheena", "Jacob"),
           pred_physhealth = exp(value) - 1) %>%
    select(names, pred_physhealth)

preds_m_16imp %>% kable(digits = 3)

names	pred_physhealth
Sheena	2.673
Jacob	12.614

16.10.4 Nomogram

We can also develop a nomogram, if we like. As a special touch, we’ll add a prediction at the bottom which back-transforms out of the predicted phys_tr back to the physhealth days.

plot(nomogram(m16_imp, 
              fun = list(function(x) exp(x) - 1),
              funlabel = "Predicted physhealth days",
              fun.at = seq(0, 30, 3)))

We can see the big role of comor and hx_depress in this model.

16.10.5 Validating Summary Statistics

We can cross-validate summary measures, like $R^2$…

validate(m16_imp)

          index.orig training   test optimism index.corrected  n
R-square      0.1975   0.2084 0.1902   0.0182          0.1793 40
MSE           1.6255   1.5967 1.6401  -0.0434          1.6688 40
g             0.6961   0.7212 0.6954   0.0258          0.6703 40
Intercept     0.0000   0.0000 0.0642  -0.0642          0.0642 40
Slope         1.0000   1.0000 0.9659   0.0341          0.9659 40