28  Multinomial Logistic Regression

28.1 R Setup Used Here

knitr::opts_chunk$set(comment = NA)

library(broom)
library(knitr)
library(MASS)
library(nnet)
library(tidyverse) 

theme_set(theme_bw())

28.1.1 Data Load

authorship <- read_csv("data/authorship.csv", show_col_types = FALSE)

28.2 The Authorship Example

This example is based on the work of Jeffrey S. Simonoff (2003) Analyzing Categorical Data in Chapter 10. Related data and R code are available at this link. Meanwhile, the data set and analysis are based on the work of Peng RD and Hengartner NW (2002) Quantitative analysis of literary styles, The American Statistician, 56, 175-185.

The authorship.csv data file contains 841 rows. Each row describes a block of text that contains 1700 total words from one of several books by four authors: Jane Austen (samples from 7 books), Jack London (6 books), John Milton (2 books), or William Shakespeare (12 books). The data include counts within the blocks of text of 69 function words, such as “a”, “by”, “no”, “that” and “with”. The goal of our analysis, mirroring that of Simonoff, will be to use the incidence of these function words to build a model that distinguishes the authors.

authorship$Author <- factor(authorship$Author, 
    levels = c("Shakespeare", "Austen", "London", "Milton"))

authorship
# A tibble: 841 × 71
   BookID Author     a   all  also    an   and   any   are    as    at    be
    <dbl> <fct>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
 1      1 Austen    46    12     0     3    66     9     4    16    13    13
 2      1 Austen    35    10     0     7    44     4     3    18    16     9
 3      1 Austen    46     2     0     3    40     1    13    11     9    23
 4      1 Austen    40     7     0     4    64     3     3    20    13    20
 5      1 Austen    29     5     0     6    52     5    14    17     6    16
 6      1 Austen    27     8     0     3    42     2    15    11    14    12
 7      1 Austen    34     8     0    15    44     2     6    16    14    11
 8      1 Austen    38     6     1     2    67     3     6    17     4    21
 9      1 Austen    34    12     0     5    50     2     8     7    13     7
10      1 Austen    54     8     0     6    44     4     8    13    17    14
# ℹ 831 more rows
# ℹ 59 more variables: been <dbl>, but <dbl>, by <dbl>, can <dbl>, do <dbl>,
#   down <dbl>, even <dbl>, every <dbl>, `for` <dbl>, from <dbl>, had <dbl>,
#   has <dbl>, have <dbl>, her <dbl>, his <dbl>, `if` <dbl>, `in` <dbl>,
#   into <dbl>, is <dbl>, it <dbl>, its <dbl>, may <dbl>, more <dbl>,
#   must <dbl>, my <dbl>, no <dbl>, not <dbl>, now <dbl>, of <dbl>, on <dbl>,
#   one <dbl>, only <dbl>, or <dbl>, our <dbl>, should <dbl>, so <dbl>, …

To-morrow, and to-morrow, and to-morrow, Creeps in this petty pace from day to day, To the last syllable of recorded time; And all our yesterdays have lighted fools The way to dusty death. Out, out, brief candle! Life’s but a walking shadow, a poor player, That struts and frets his hour upon the stage, And then is heard no more. It is a tale Told by an idiot, full of sound and fury, Signifying nothing.

28.3 Focus on 11 key words

Again, following Simonoff, we will focus on 11 words from the set of 69 potential predictors in the data, specifically…

  • “be”, “been”, “had”, “it”, “may”, “not”, “on”, “the”, “upon”, “was” and “which”
auth2 <- authorship |>
    select(Author, BookID, be, been, had, it, may, not, 
           on, the, upon, was, which)

auth2.long <- auth2 |>
    gather("word", "n", 3:13)

auth2.long
# A tibble: 9,251 × 4
   Author BookID word      n
   <fct>   <dbl> <chr> <dbl>
 1 Austen      1 be       13
 2 Austen      1 be        9
 3 Austen      1 be       23
 4 Austen      1 be       20
 5 Austen      1 be       16
 6 Austen      1 be       12
 7 Austen      1 be       11
 8 Austen      1 be       21
 9 Austen      1 be        7
10 Austen      1 be       14
# ℹ 9,241 more rows

28.3.1 Side by Side Boxplots

ggplot(auth2.long, aes(x = Author, y = n)) +
    geom_boxplot() +
    facet_wrap(~ word, ncol = 3, scales = "free_y") + 
    labs(x = "", y = "")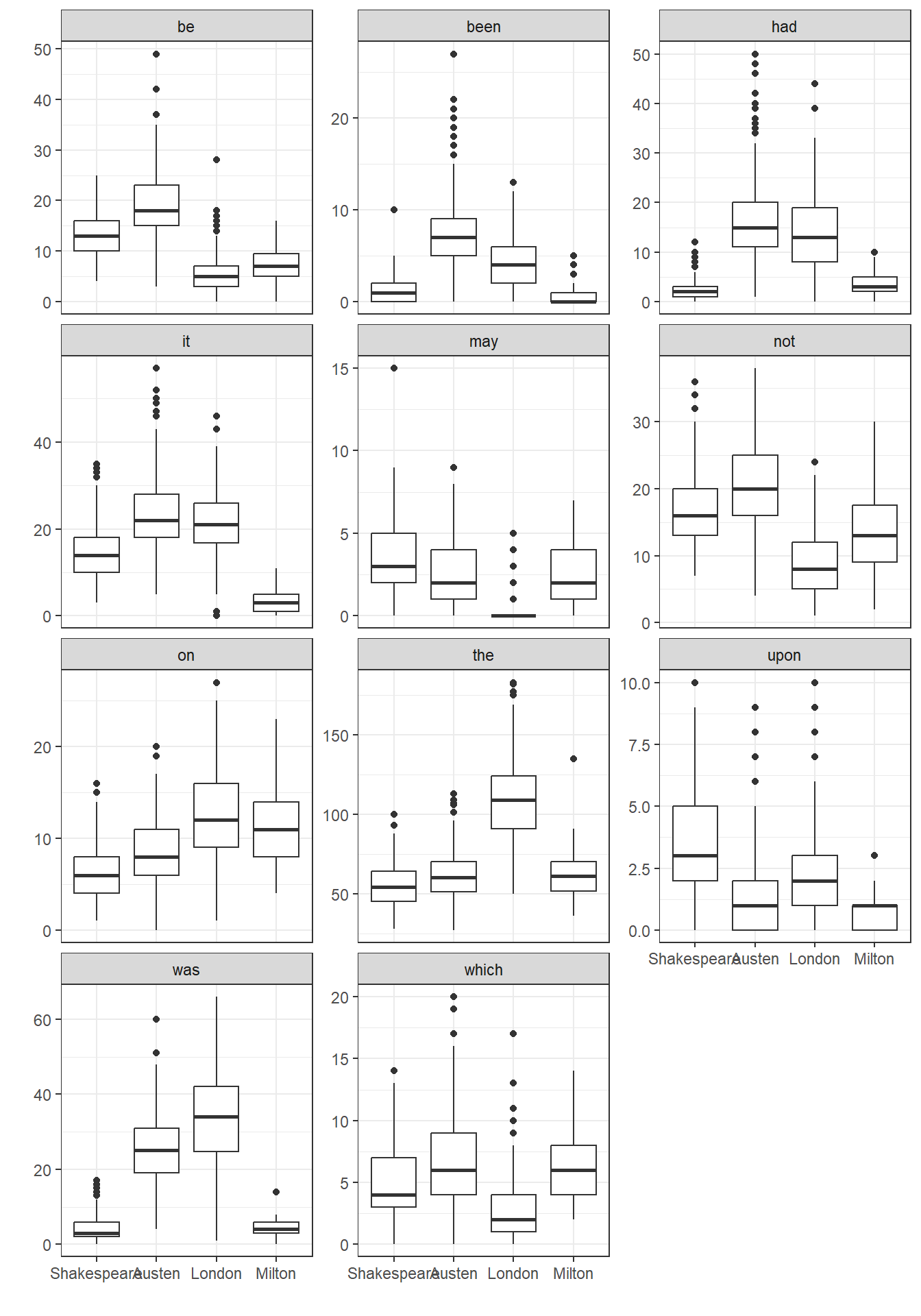

Oh! do not attack me with your watch. A watch is always too fast or too slow. I cannot be dictated to by a watch.

28.4 A Multinomial Logistic Regression Model

Let’s start with a multinomial model to predict Author on the basis of these 11 key predictors, using the multinom function from the nnet package.

authnom1 <- multinom(Author ~ be + been + had + it + may + not + on + 
                         the + upon + was + which, data=authorship, 
                     maxit=200)
# weights:  52 (36 variable)
initial  value 1165.873558 
iter  10 value 293.806160
iter  20 value 273.554538
iter  30 value 192.309644
iter  40 value 71.091334
iter  50 value 48.419335
iter  60 value 46.808141
iter  70 value 46.184752
iter  80 value 46.026162
iter  90 value 45.932823
iter 100 value 45.897793
iter 110 value 45.868017
iter 120 value 45.863256
final  value 45.863228 
converged
summary(authnom1)
Call:
multinom(formula = Author ~ be + been + had + it + may + not + 
    on + the + upon + was + which, data = authorship, maxit = 200)

Coefficients:
       (Intercept)          be       been       had          it         may
Austen  -15.504834  0.48974946  0.5380318 0.4620513  0.00388835 -0.15025084
London  -14.671720 -0.07497073  0.1733116 0.4842272  0.08674782 -0.01590702
Milton   -1.776866 -0.10891178 -0.9127155 0.5319573 -0.82046587 -0.06760436
               not        on         the      upon       was       which
Austen -0.08861462 0.5967404 -0.02361614 -2.119001 0.7021371  0.10370827
London -0.32567063 0.5749969  0.12039782 -1.914428 0.6767581 -0.59121054
Milton  0.05575887 0.5198173  0.08739368 -2.042475 0.3048202 -0.05939104

Std. Errors:
       (Intercept)        be      been       had         it       may       not
Austen    4.892258 0.1643694 0.3117357 0.2695081 0.09554376 0.3008164 0.1078329
London    5.372898 0.1916618 0.3308759 0.2812555 0.11355697 0.4946804 0.1440760
Milton    5.417300 0.1613282 0.5910561 0.3187304 0.23015421 0.3500753 0.1309306
              on        the      upon       was     which
Austen 0.2213827 0.03457288 0.6426484 0.1808681 0.1646472
London 0.2251642 0.03088881 0.7072129 0.1768901 0.2542886
Milton 0.2223575 0.04783646 0.6436399 0.1820885 0.2111105

Residual Deviance: 91.72646 
AIC: 163.7265

28.4.1 Testing Model 1

z1 <- summary(authnom1)$coefficients/summary(authnom1)$standard.errors
round(z1,2)
       (Intercept)    be  been  had    it   may   not   on   the  upon  was
Austen       -3.17  2.98  1.73 1.71  0.04 -0.50 -0.82 2.70 -0.68 -3.30 3.88
London       -2.73 -0.39  0.52 1.72  0.76 -0.03 -2.26 2.55  3.90 -2.71 3.83
Milton       -0.33 -0.68 -1.54 1.67 -3.56 -0.19  0.43 2.34  1.83 -3.17 1.67
       which
Austen  0.63
London -2.32
Milton -0.28
p1 <- (1 - pnorm(abs(z1), 0, 1)) * 2
kable(round(p1,3))
(Intercept) be been had it may not on the upon was which
Austen 0.002 0.003 0.084 0.086 0.968 0.617 0.411 0.007 0.495 0.001 0.000 0.529
London 0.006 0.696 0.600 0.085 0.445 0.974 0.024 0.011 0.000 0.007 0.000 0.020
Milton 0.743 0.500 0.123 0.095 0.000 0.847 0.670 0.019 0.068 0.002 0.094 0.778

Simonoff suggests that “been” and “may” can be dropped. What do we think?

The proper function of man is to live, not to exist. I shall not waste my days in trying to prolong them. I shall use my time.

28.5 Model 2

authnom2 <- multinom(Author ~ be + had + it + not + on + 
                         the + upon + was + which, data=authorship, 
                     maxit=200)
# weights:  44 (30 variable)
initial  value 1165.873558 
iter  10 value 304.985478
iter  20 value 285.428679
iter  30 value 143.301103
iter  40 value 54.589791
iter  50 value 52.140470
iter  60 value 51.421454
iter  70 value 51.012790
iter  80 value 50.888718
iter  90 value 50.834262
iter 100 value 50.743136
final  value 50.743111 
converged
summary(authnom2)
Call:
multinom(formula = Author ~ be + had + it + not + on + the + 
    upon + was + which, data = authorship, maxit = 200)

Coefficients:
       (Intercept)          be       had          it         not        on
Austen   -16.55647  0.45995950 0.6698612  0.02621612 -0.03684654 0.4676716
London   -16.06419 -0.13378141 0.6052164  0.10517792 -0.27934022 0.4958923
Milton    -2.22344 -0.07031256 0.1737526 -0.81984885  0.05444678 0.5363108
                the      upon       was       which
Austen -0.001852454 -1.950761 0.6543956  0.06363998
London  0.128565811 -1.643829 0.6418607 -0.54690144
Milton  0.074236636 -1.762533 0.2932065 -0.08748272

Std. Errors:
       (Intercept)        be       had         it        not        on
Austen    4.723001 0.1293729 0.2201823 0.08657746 0.08771157 0.1949021
London    5.202732 0.1587639 0.2306803 0.10117217 0.11608348 0.2072383
Milton    4.593806 0.1499103 0.2057258 0.21551377 0.12103678 0.1895226
              the      upon       was     which
Austen 0.02945139 0.5620273 0.1524982 0.1466250
London 0.02739965 0.6219927 0.1512911 0.2087120
Milton 0.04463721 0.6246766 0.1601393 0.1928361

Residual Deviance: 101.4862 
AIC: 161.4862

28.5.1 Comparing Model 2 to Model 1

anova(authnom1, authnom2)
Likelihood ratio tests of Multinomial Models

Response: Author
                                                             Model Resid. df
1              be + had + it + not + on + the + upon + was + which      2493
2 be + been + had + it + may + not + on + the + upon + was + which      2487
  Resid. Dev   Test    Df LR stat.   Pr(Chi)
1  101.48622                                
2   91.72646 1 vs 2     6 9.759767 0.1351402

28.5.2 Testing Model 2

z2 <- summary(authnom2)$coefficients/summary(authnom2)$standard.errors
round(z2,2)
       (Intercept)    be  had    it   not   on   the  upon  was which
Austen       -3.51  3.56 3.04  0.30 -0.42 2.40 -0.06 -3.47 4.29  0.43
London       -3.09 -0.84 2.62  1.04 -2.41 2.39  4.69 -2.64 4.24 -2.62
Milton       -0.48 -0.47 0.84 -3.80  0.45 2.83  1.66 -2.82 1.83 -0.45
p2 <- (1 - pnorm(abs(z2), 0, 1)) * 2
round(p2,3)
       (Intercept)    be   had    it   not    on   the  upon   was which
Austen       0.000 0.000 0.002 0.762 0.674 0.016 0.950 0.001 0.000 0.664
London       0.002 0.399 0.009 0.299 0.016 0.017 0.000 0.008 0.000 0.009
Milton       0.628 0.639 0.398 0.000 0.653 0.005 0.096 0.005 0.067 0.650

28.5.3 A little history

Simonoff has an interesting note: Consider the lifetimes of these four authors:

  • William Shakespeare was born in 1564 and died in 1616
  • John Milton was born in 1608 (44 years after Shakespeare) and died in 1674
  • Jane Austen was born in 1775 (211 years after Shakespeare) and died in 1817
  • Jack London was born in 1876 (312 years after Shakespeare) and died in 1916

How many large coefficients does each author display relative to Shakespeare?

28.6 Classification Table

How well does this model (model 2) distinguish these authors based on blocks of 1700 words of text?

table(authorship$Author, predict(authnom2))
             
              Shakespeare Austen London Milton
  Shakespeare         168      3      1      1
  Austen                4    308      5      0
  London                0      1    294      1
  Milton                2      0      1     52

Based on this classification table, I’d say it does a nice job. Almost 98% of the blocks of text are correctly classified.

Fly, envious Time, till thou run out thy race; Call on the lazy leaden-stepping hours, Whose speed is but the heavy plummet’s pace; And glut thyself with what thy womb devours, Which is no more then what is false and vain, And merely mortal dross; So little is our loss, So little is thy gain. For when, as each thing bad thou hast entomb’d And last of all thy greedy self consumed, Then long Eternity shall greet our bliss, With an individual kiss; And Joy shall overtake us, as a flood, When every thing that is sincerely good, And perfectly divine, With truth, and peace, and love, shall ever shine, About the supreme throne Of Him, to whose happy-making sight, alone, When once our heavenly-guided soul shall climb, Then all this earthly grossness quit, Attired with stars, we shall for ever sit, Triumphing over Death, and Chance, and thee, O Time!

28.7 Probability Curves based on a Single Predictor

In situations where only one predictor is used, we can develop nice plots of estimated probabilities for each group as a function of the predictor. Suppose we look at the single word “been” (note that this was left out of Model 2.)

Note that the possible values for counts of “been” in the data range from 0 to 27…

summary(authorship$been)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.000   2.000   4.000   4.614   7.000  27.000

Now, we’ll build a model to predict the author based solely on the counts of the word “been”.

authnom3 <- multinom(Author ~ been, 
                     data=authorship, maxit=200)
# weights:  12 (6 variable)
initial  value 1165.873558 
iter  10 value 757.915093
iter  20 value 755.454631
final  value 755.454551 
converged

Next, we’ll build a grid of the predicted log odds for each author (as compared to Shakespeare) using the fitted coefficients. The grid will cover every possible value from 0 to 27, increasing by 0.1, using the following trick in R.

beengrid <- cbind(1,c(0:270)/10)
austenlogit <- beengrid %*% coef(authnom3)[1,]
londonlogit <- beengrid %*% coef(authnom3)[2,]
miltonlogit <- beengrid %*% coef(authnom3)[3,]

Next, we’ll use that grid of logit values to estimate the fitted probabilities for each value of “been” between 0 and 27.

austenprob <- exp(austenlogit)/ 
    (exp(austenlogit) + exp(londonlogit) + 
         exp(miltonlogit) + 1)
londonprob <- exp(londonlogit)/ 
    (exp(austenlogit) + exp(londonlogit) + 
         exp(miltonlogit) + 1)
miltonprob <- exp(miltonlogit)/ 
    (exp(austenlogit) + exp(londonlogit) + 
         exp(miltonlogit) + 1)
shakesprob <- 1 - austenprob - londonprob - miltonprob

been_dat <- data_frame(been_count = beengrid[,2], 
                       austen = austenprob[,1], 
                       london = londonprob[,1], 
                       milton = miltonprob[,1], 
                       shakespeare = shakesprob[,1])
Warning: `data_frame()` was deprecated in tibble 1.1.0.
ℹ Please use `tibble()` instead.
been_dat
# A tibble: 271 × 5
   been_count austen london milton shakespeare
        <dbl>  <dbl>  <dbl>  <dbl>       <dbl>
 1        0   0.0258  0.136  0.285       0.553
 2        0.1 0.0288  0.147  0.272       0.553
 3        0.2 0.0321  0.158  0.258       0.551
 4        0.3 0.0357  0.171  0.245       0.548
 5        0.4 0.0396  0.184  0.232       0.545
 6        0.5 0.0438  0.197  0.219       0.540
 7        0.6 0.0484  0.211  0.207       0.534
 8        0.7 0.0534  0.225  0.195       0.527
 9        0.8 0.0587  0.240  0.183       0.518
10        0.9 0.0644  0.256  0.171       0.509
# ℹ 261 more rows

Now, we gather the data by author name and probability

been_dat_long <- been_dat |>
    gather("name", "prob", 2:5)
been_dat_long
# A tibble: 1,084 × 3
   been_count name     prob
        <dbl> <chr>   <dbl>
 1        0   austen 0.0258
 2        0.1 austen 0.0288
 3        0.2 austen 0.0321
 4        0.3 austen 0.0357
 5        0.4 austen 0.0396
 6        0.5 austen 0.0438
 7        0.6 austen 0.0484
 8        0.7 austen 0.0534
 9        0.8 austen 0.0587
10        0.9 austen 0.0644
# ℹ 1,074 more rows

28.7.1 Produce the Plot of Estimated Probabilities based on “been” counts

ggplot(been_dat_long, aes(x = been_count, y = prob, 
                          col = name)) +
    geom_line(linewidth = 1.5) +
    labs(x = "Count of the word `been`", 
         y = "Model probability")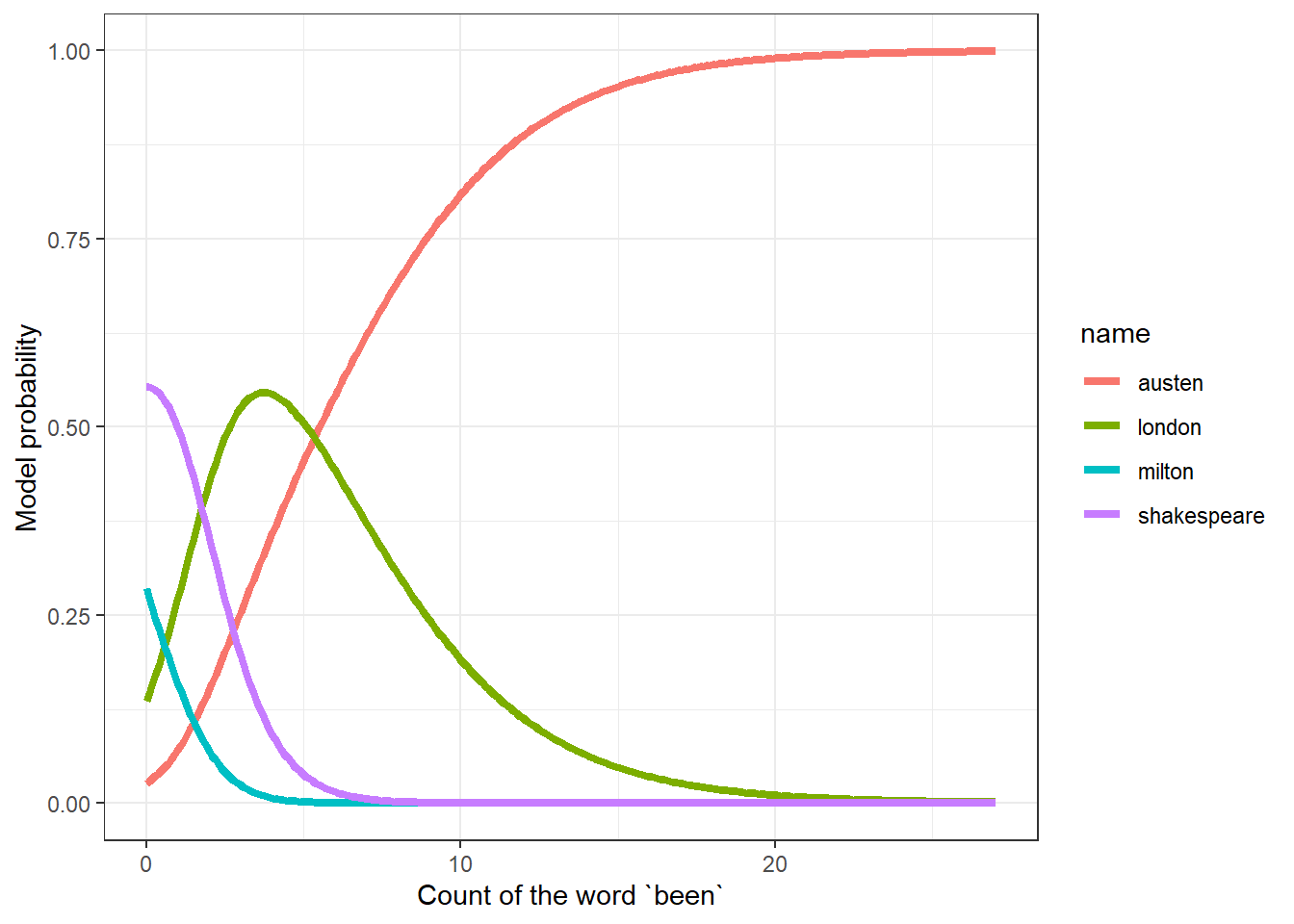

28.7.2 Boxplot of “been” counts

Compare this to what we see in the raw counts of the word “been”.

been.long <- filter(auth2.long, word == "been")
been.long$Auth <- fct_relevel(been.long$Author, 
            "Austen", "London", "Milton", "Shakespeare")
# releveling to make the colors match the model plot

ggplot(been.long, aes(x = Auth, y = n, fill = Auth)) +
    geom_boxplot() +
    guides(fill = "none") +
    labs(x = "", y = "Count of the word `been`")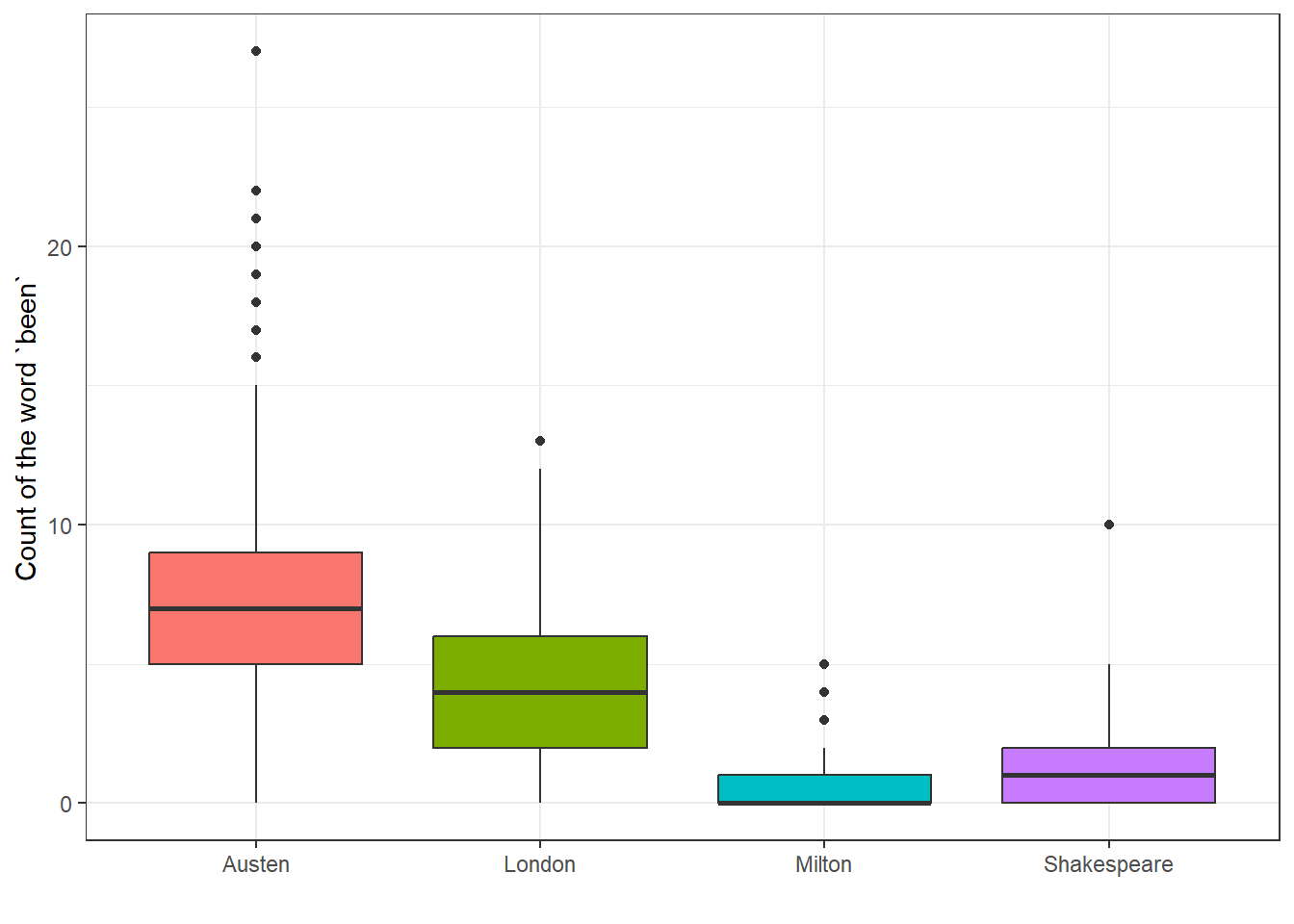

28.7.3 Quote Sources

  1. To-morrow, and to-morrow, and to-morrow … Shakespeare Macbeth Act 5.
  2. Oh! do not attack me with your watch. … Jane Austen Mansfield Park
  3. The proper function of man is to live, not to exist. … Jack London The Bulletin San Francisco 1916-12-02.
  4. Fly, envious Time, till thou run out thy race … John Milton On Time