7  Transformation

7.1 R setup for this chapter

Note

Appendix A lists all R packages used in this book, and also provides R session information. Appendix B describes the 431-Love.R script, and demonstrates its use.

7.2 Data from an .Rds file: DARWIN data

Note

Appendix C provides further guidance on pulling data from other systems into R, while Appendix D gives more information (including download links) for all data sets used in this book.

The DARWIN dataset (Diagnosis AlzheimeR WIth haNdwriting) includes handwriting data specifically designed for the early detection of Alzheimer’s disease (AD). These data are found in the UC Irvine Machine Learning Repository and are derived from Cilia et al. (2022). Gathered into our darwin.Rds file are times to complete three handwriting tasks sampled from the original protocol of 25 such tasks:

  • task 1 (a signature),
  • task 3 (joining points with a vertical line four times) and
  • task 25 (copying a 110-character paragraph)

The .Rds file we have is an R data set, which we can ingest directly with read_rds().

darwin <- read_rds("data/darwin.Rds")

darwin
# A tibble: 174 × 5
   subject status time01 time03 time25
   <chr>   <fct>   <dbl>  <dbl>  <dbl>
 1 S_001   HC       5870  10845  61885
 2 S_002   AD       7840  12260  41990
 3 S_003   AD     156085  20205 159395
 4 S_004   AD       4160   3190  77170
 5 S_005   HC       6870  10400 124760
 6 S_006   AD       5685   5455 252180
 7 S_007   HC       5790   2195  36845
 8 S_008   AD       8445  10735 106760
 9 S_009   AD       9450  24140  72085
10 S_010   AD      17625   8790 122115
# ℹ 164 more rows
n_miss(darwin)
[1] 0

Our data describe 5 characteristics, including a subject ID (subject) for each of 174 study participants. While the units of time are not clearly specified, they seem to be milliseconds, so, for example, the first subject completed task 1 in 5.87 seconds (5870 ms.) We see also that there are no missing values in the darwin data.

Note that the status variable takes two values:

  • HC for Healthy Control
  • AD for subject with Alzheimer’s Disease.
darwin |> count(status)
# A tibble: 2 × 2
  status     n
  <fct>  <int>
1 HC        85
2 AD        89

In the rest of this chapter, we will explore the comparison of each of the three task times (gathered in time01, time03 and time 25) between the subjects with Alzheimer’s Disease and the Healthy Controls.

7.3 Visualizing the data for Task 3

In looking at the data for Task 3, we have two independent samples of an outcome (time03) split into two groups by status.

darwin |>
  reframe(lovedist(time03), .by = status)
# A tibble: 2 × 11
  status     n  miss   mean    sd   med   mad   min   q25   q75   max
  <fct>  <int> <int>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 HC        85     0  7477. 4297.  6585 3306.   460  4830  9390 32795
2 AD        89     0 13589. 8183. 12070 7502.   895  7180 17605 39545

A plot of the data, like the one below, shows some right skew within each group, specifically a few times that are much longer than the rest. Does a comparison of sample means (shown as gold dots) seem particularly appropriate in this setting?

ggplot(darwin, aes(y = status, x = time03, fill = status)) +
  stat_slab(aes(thickness = after_stat(pdf * n)), scale = 0.7) +
  stat_dotsinterval(side = "bottom", scale = 0.7, slab_linewidth = NA) +
  stat_summary(fun = mean, geom = "point", size = 3, col = "gold") +
  scale_fill_metro_d() +
  guides(fill = "none") +
  labs(x = "Time to complete Task 3 (in ms)")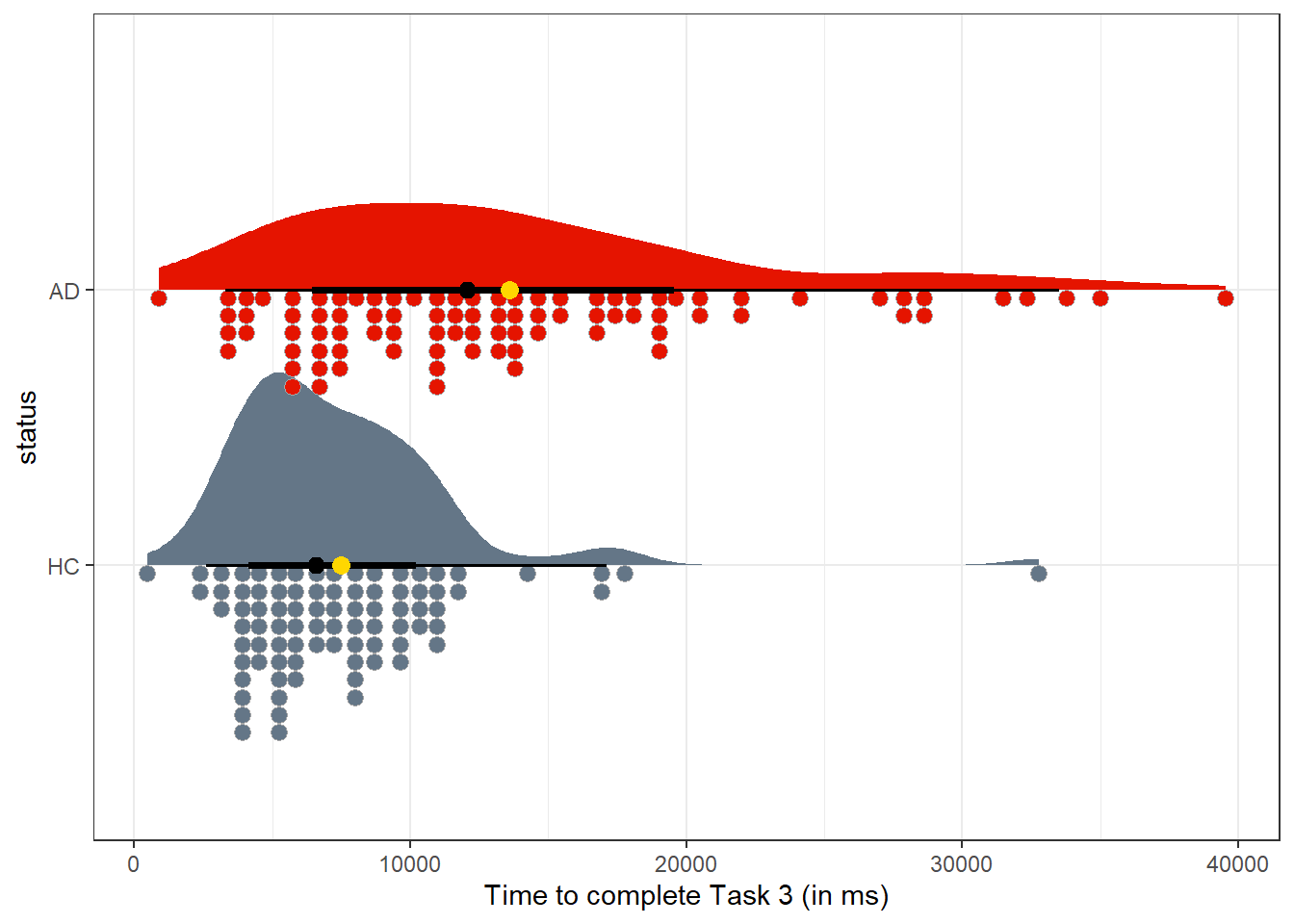

Our approaches for inference about two independent samples mostly anticipate a more symmetric distribution (with less substantial outliers and with the mean closer to the median) in each sample. Could we transform the data on time to complete Task 3 so as to obtain a comparison which might fit those assumptions?

7.4 Some Linear Transformations

Some commonly used transformations in statistics do not change the shape of our distribution in any meaningful way. These are linear transformations, where our transformed data is just a linear function of the original data.

Examples include:

  • centering the data, by subtracting away its mean, so that the mean value of our transformed data becomes zero, which can be accomplished with the center() function from the datawizard package in easystats.
dat1 <- darwin |> mutate(ctime03 = center(time03))

dat1 |>
  reframe(lovedist(time03)) |>
  kable(digits = 2)
n miss mean sd med mad min q25 q75 max
174 0 10603.36 7239.98 8585 4866.63 460 5568.75 13443.75 39545 
dat1 |>
  reframe(lovedist(ctime03)) |>
  kable(digits = 2)
n miss mean sd med mad min q25 q75 max
174 0 0 7239.98 -2018.36 4866.63 -10143.36 -5034.61 2840.39 28941.64
  • rescaling the data to a new range, through division by a constant value, which can be accomplished by setting the desired minimum and maximum values with the rescale() function from the datawizard package in easystats.
dat1 <- dat1 |> mutate(rstime03 = rescale(time03, to = c(0, 100)))

dat1 |>
  reframe(lovedist(rstime03)) |>
  kable(digits = 2)
n miss mean sd med mad min q25 q75 max
174 0 25.95 18.52 20.79 12.45 0 13.07 33.22 100
  • standardizing the data, which involves both subtracting the mean and dividing by the standard deviation, to produce new data with a mean of 0 and a standard deviation of 1 (this is sometimes referred to as Z-scoring or normalization.) Here, we’ll use the standardize() function from the datawizard package in easystats.
dat1 <- dat1 |> mutate(ztime03 = standardize(time03))

dat1 |>
  reframe(lovedist(ztime03)) |>
  kable(digits = 2)
n miss mean sd med mad min q25 q75 max
174 0 0 1 -0.28 0.67 -1.4 -0.7 0.39 4

Note, however, that none of these linear transformations fix our problem with the shape of our distribution.

p1 <- ggplot(dat1, aes(x = time03, y = status)) +
  geom_boxplot() +
  labs(title = "Original Time03 data")

p2 <- ggplot(dat1, aes(x = ctime03, y = status)) +
  geom_boxplot() +
  labs(title = "Centered Time03 data")

p3 <- ggplot(dat1, aes(x = rstime03, y = status)) +
  geom_boxplot() +
  labs(title = "Rescaled Time03 data")

p4 <- ggplot(dat1, aes(x = ztime03, y = status)) +
  geom_boxplot() +
  labs(title = "Standardized Time03 data")

(p1 + p2) / (p3 + p4) +
  plot_annotation(title = "Linear Transformations don't change the shape of a distribution.")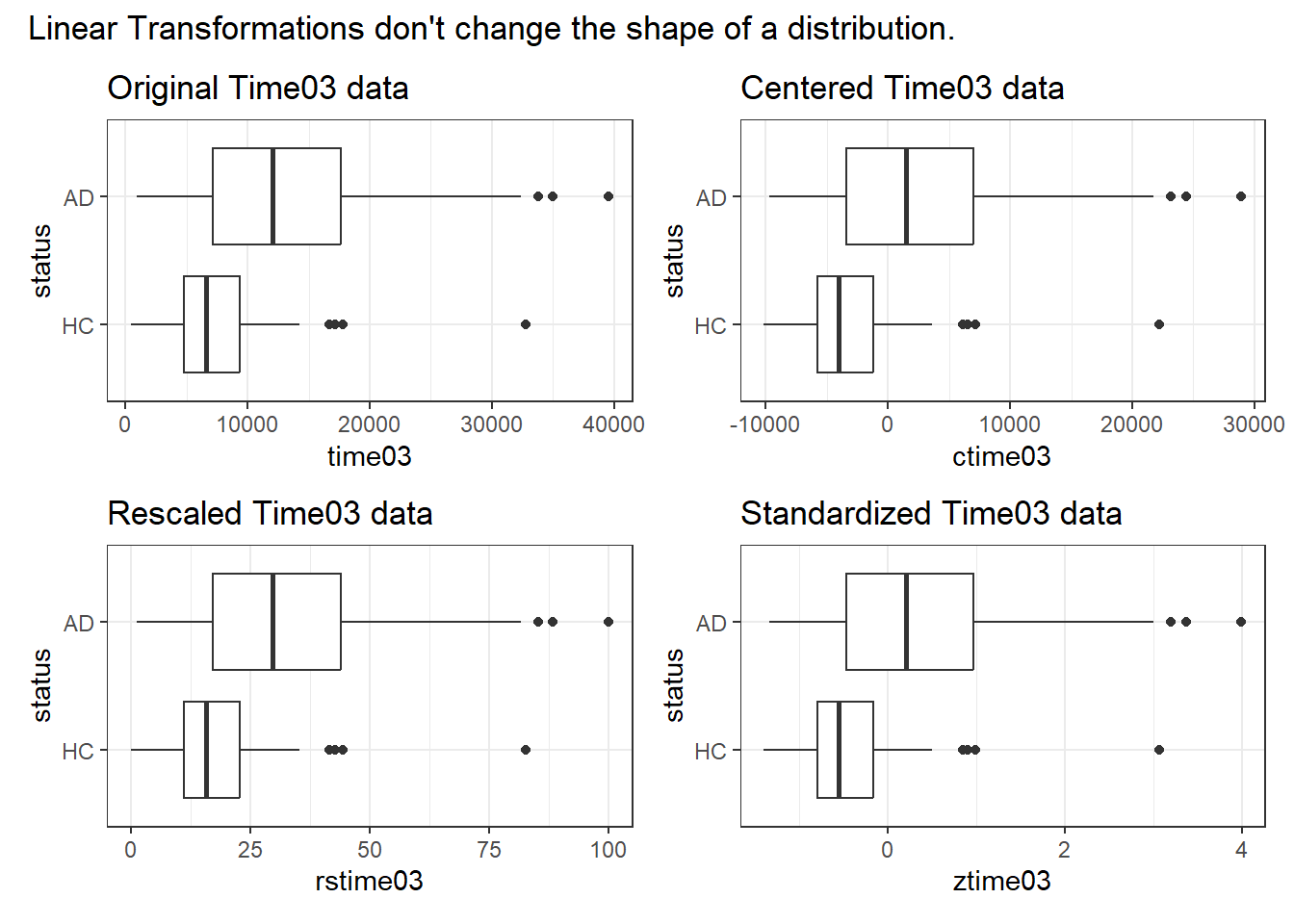

So these linear transformations may slide the distribution back-and-forth along the x axis, and may expand or contract the range of that distribution, but they don’t address the problems we’ve had with the shape of the data.

We need to think about some potential transformations that don’t just add/subtract or multiply/divide by a constant. We need something non-linear.

7.5 The Logarithmic Transformation

The logarithm is one of the more useful non-linear transformations, when our data (as in this case) are entirely positive and show signs of right skew. In R (and in this class), the log() function refers to the natural logarithm, with base \(e\), rather than log10(), which produces the base 10 logarithm. Either can be used to accomplish the same sort of reshaping of our data.

p1 <- ggplot(darwin, aes(x = time03, y = status)) +
  geom_boxplot() +
  stat_summary(geom = "point", fun = "mean", size = 2, col = "red") +
  labs(title = "Original Time03 data")

p2 <- ggplot(darwin, aes(x = log(time03), y = status)) +
  geom_boxplot() +
  stat_summary(geom = "point", fun = "mean", size = 2, col = "red") +
  labs(title = "Natural log of Time03")

p3 <- ggplot(darwin, aes(x = log10(time03), y = status)) +
  geom_boxplot() +
  stat_summary(geom = "point", fun = "mean", size = 2, col = "red") +
  labs(title = "Base 10 log of Time03")

p1 / p2 / p3 +
  plot_annotation(title = "Logarithmic transformations affect the shape of a distribution.")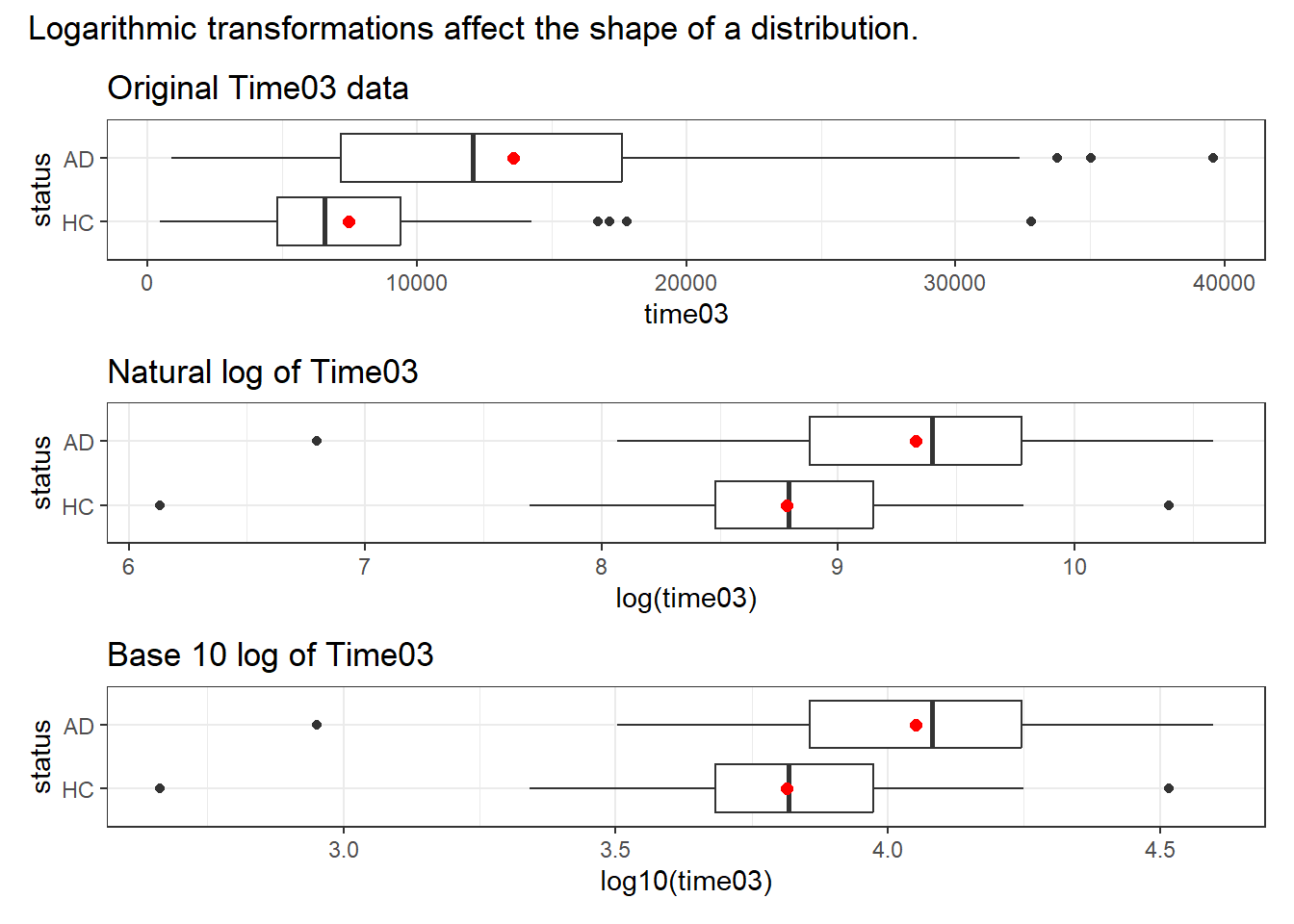

Note
  1. Each of the logged time distributions are more symmetric (much less right-skewed, with the mean closer to the median) than our original data.
  2. The two logarithmic bases, though they produce different scales, produce the same distributional shapes as each other.
darwin |>
  reframe(lovedist(time03), .by = status) |>
  kable(digits = 2)
status n miss mean sd med mad min q25 q75 max
HC 85 0 7476.88 4297.36 6585 3306.20 460 4830 9390 32795
AD 89 0 13589.33 8182.96 12070 7501.96 895 7180 17605 39545 
darwin |>
  reframe(lovedist(log(time03)), .by = status) |>
  kable(digits = 2)
status n miss mean sd med mad min q25 q75 max
HC 85 0 8.78 0.55 8.79 0.52 6.13 8.48 9.15 10.40
AD 89 0 9.33 0.66 9.40 0.66 6.80 8.88 9.78 10.59 
darwin |>
  reframe(lovedist(log10(time03)), .by = status) |>
  kable(digits = 2)
status n miss mean sd med mad min q25 q75 max
HC 85 0 3.81 0.24 3.82 0.22 2.66 3.68 3.97 4.52
AD 89 0 4.05 0.29 4.08 0.28 2.95 3.86 4.25 4.60

7.5.1 Importance of the Log Transformation

— from Gelman, Hill, and Vehtari (2021)

The line y = a + bx can be used to express a more general class of relationships by allowing logarithmic transformations. The formula log y = a + bx represents exponential growth (if b > 0) or decline (if b < 0*): y = A exp(bx) where A = exp(a). The parameter A is the value of y when x = 0 and the parameters b determines the rate of growth or decline. A one-unit difference in x corresponds to an additive difference of b in log y and thus a multiplicative factor of exp(b) in y.

It is often helpful to model all-positive random variables on the logarithmic scale because it does not allow for values that are 0 or negative. The logarithmic transformation is non-linear and it pulls in the values at the high end, compressing the scale of the distribution.

7.6 Box-Cox to suggest Power Transformations

There are several other non-linear transformations we might consider in this situation, including an entire family of power distributions. Tukey’s ladder of power transformations can guide our exploration.

Power (\(\lambda\)) -2 -1 -1/2 0 1/2 1 2
Transformation 1/y2 1/y 1/\(\sqrt{y}\) log y \(\sqrt{y}\) y y2

The Box-Cox plot, sifts through the ladder of options to suggest a transformation (for our outcome) to achieve a more Normal distribution within each group, and linearize the outcome-predictor(s) relationship.

Here’s how we might fit a Box-Cox plot to our data on Task 3.

fit3 <- lm(time03 ~ status, data = darwin)
boxCox(fit3, main = "Transformations of time03")

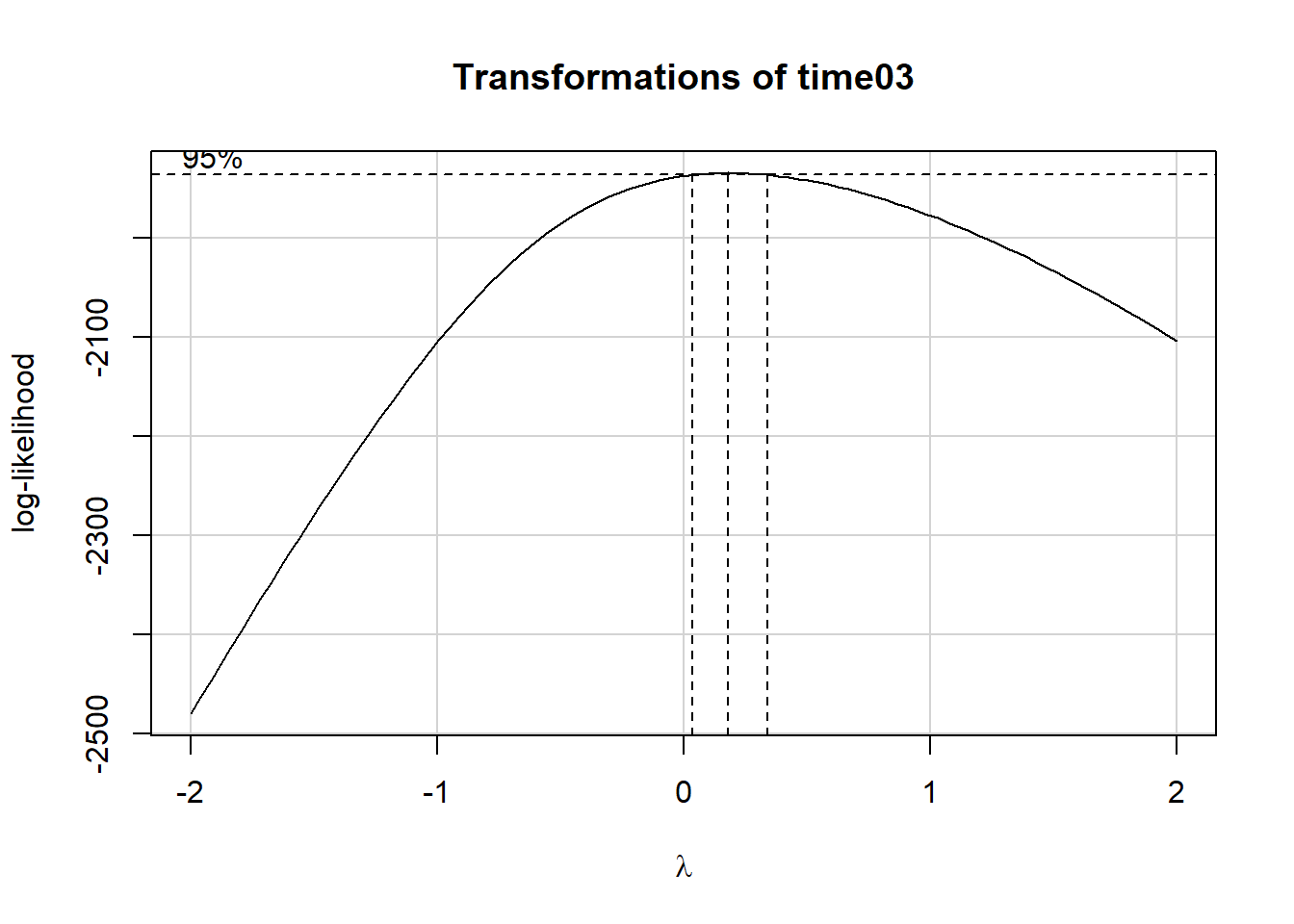
summary(powerTransform(fit3))$result
   Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Y1 0.1836012        0.33   0.03146328    0.3357392

The power transformations which the Box-Cox plots suggests here has a power of 0.33, in other words, the cube root of our outcome. But note that the logarithm (power = 0) and square root (power = 0.5) surround this option, and in the interests of simplicity, I’d like to stick to one of those two options. First, I’ll show the log transformation…

p1 <- ggplot(darwin, aes(x = log(time03), y = status)) +
  geom_boxplot() +
  stat_summary(geom = "point", fun = "mean", size = 2, col = "red") +
  labs(title = "Log of Time for Task 3")

p2 <- ggplot(darwin, aes(y = status, x = log(time03), fill = status)) +
  stat_slab(aes(thickness = after_stat(pdf * n)), scale = 0.7) +
  stat_dotsinterval(side = "bottom", scale = 0.7, slab_linewidth = NA) +
  stat_summary(fun = mean, geom = "point", size = 3, col = "gold") +
  scale_fill_metro_d() +
  guides(fill = "none") +
  labs(x = "Log of Time for Task 3")

p1 / p2 +
  plot_annotation(title = "Log of Time for Task 3")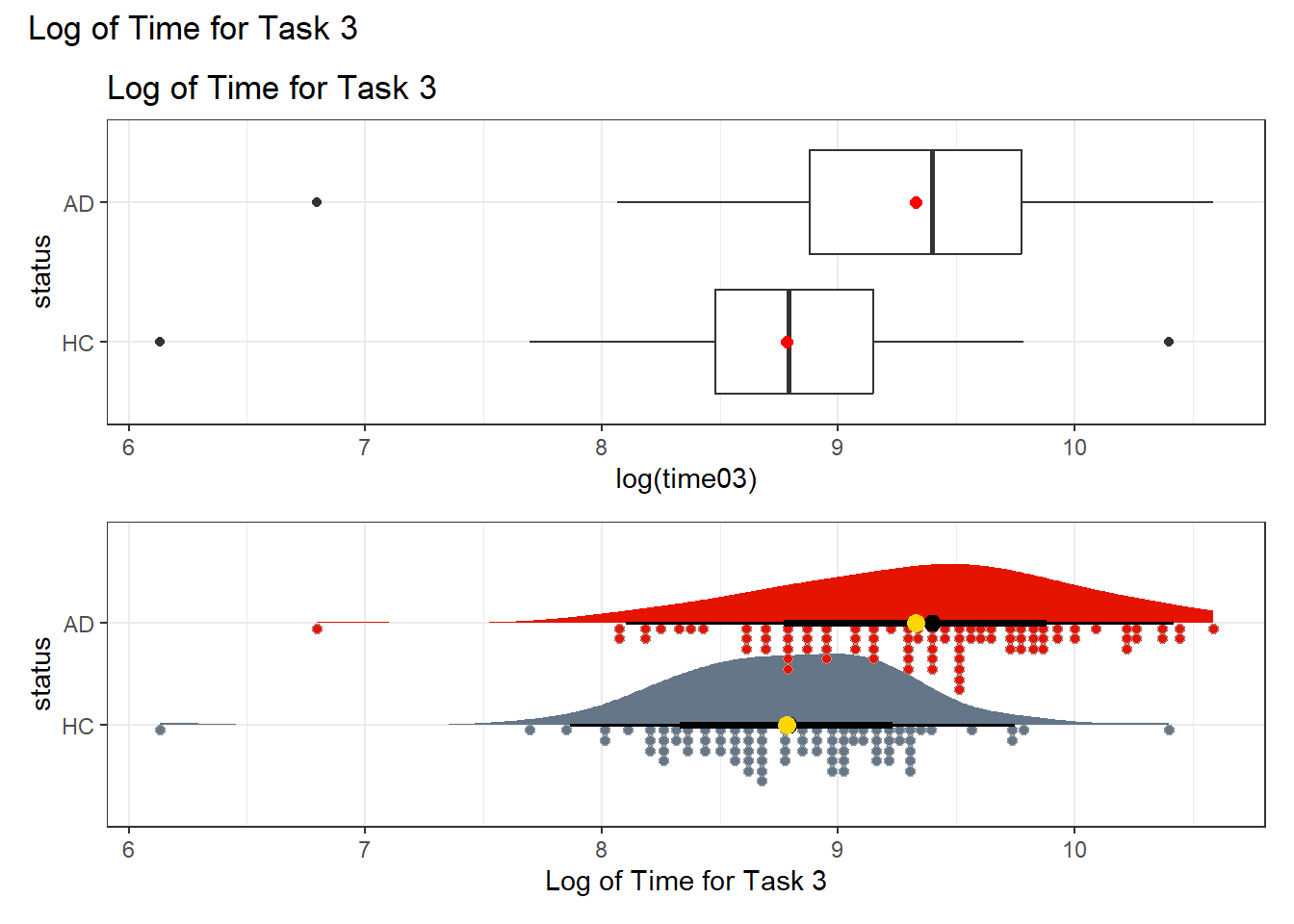

Now, let’s look at the square root transformation instead of the logarithm. Is this a meaningful improvement in terms of adherence to the assumptions required for making a comparison about the means?

p3 <- ggplot(darwin, aes(x = sqrt(time03), y = status)) +
  geom_boxplot() +
  stat_summary(geom = "point", fun = "mean", size = 2, col = "red") +
  labs(title = "Square root of Time for Task 3")

p4 <- ggplot(darwin, aes(y = status, x = sqrt(time03), fill = status)) +
  stat_slab(aes(thickness = after_stat(pdf * n)), scale = 0.7) +
  stat_dotsinterval(side = "bottom", scale = 0.7, slab_linewidth = NA) +
  stat_summary(fun = mean, geom = "point", size = 3, col = "gold") +
  scale_fill_metro_d() +
  guides(fill = "none") +
  labs(x = "Square root of Time for Task 3")

p3 / p4 +
  plot_annotation(title = "Square root of Time for Task 3")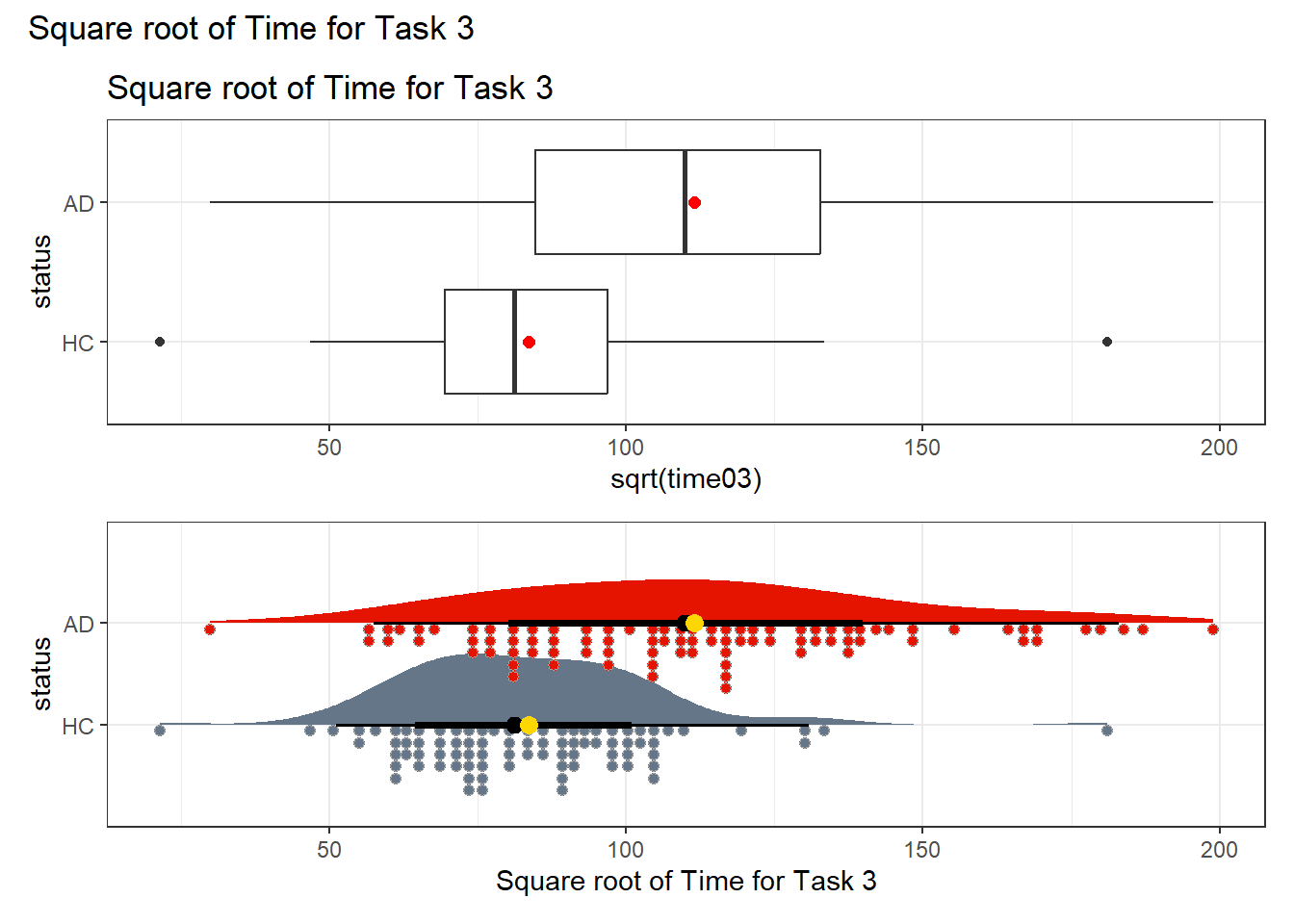

It seems that either transformation (the square root or the logarithm) can do a pretty good job of generating distributions for the two status groups (AD and HC) which are less skewed, and have fewer outliers. I’ll opt to use the logarithm here, because it is such a common choice for transformations in regression, but the square root would also work well in this specific instance.

7.6.1 A Few Caveats

  1. Some of these transformations (like the logarithm) require the data to be positive. We can rescale the Y data by adding a constant to every observation in a data set without changing shape.
  2. We can use a natural logarithm (log in R), a base 10 logarithm (log10) or even sometimes a base 2 logarithm (log2) to good effect in Tukey’s ladder. All affect the association’s shape in the same way, so we’ll stick with log (base e).
  3. Some re-expressions don’t lead to easily interpretable results. Not many things that make sense in their original units also make sense in inverse square roots. There are times when we won’t care, but often, we will.
  4. If our primary interest is in making predictions, we’ll generally be more interested in getting good predictions back on the original scale, and we can back-transform the point and interval estimates to accomplish this.

7.7 Making Inferences about Task 3

So, we’ll transform our Task 3 times by taking their logarithms.

darwin <- darwin |> mutate(logtime03 = log(time03))

This produces means in the two exposure groups which are 8.8 and 9.3 for the HC and AD groups, respectively, with standard deviations of 0.55 and 0.66, respectively. It’s appealing to be comparing transformed values which are between 0 and 100 in practice, and so we’ll look to build transformations which accomplish this aim.

darwin |> group_by(status) |> reframe(lovedist(logtime03))
# A tibble: 2 × 11
  status     n  miss  mean    sd   med   mad   min   q25   q75   max
  <fct>  <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 HC        85     0  8.78 0.551  8.79 0.516  6.13  8.48  9.15  10.4
2 AD        89     0  9.33 0.656  9.40 0.656  6.80  8.88  9.78  10.6

7.8 Linear Model and Ordinary Least Squares

To start, we’ll use ordinary least squares and a model fit with lm() to compare the logged times to complete Task 3 across the two status groups.

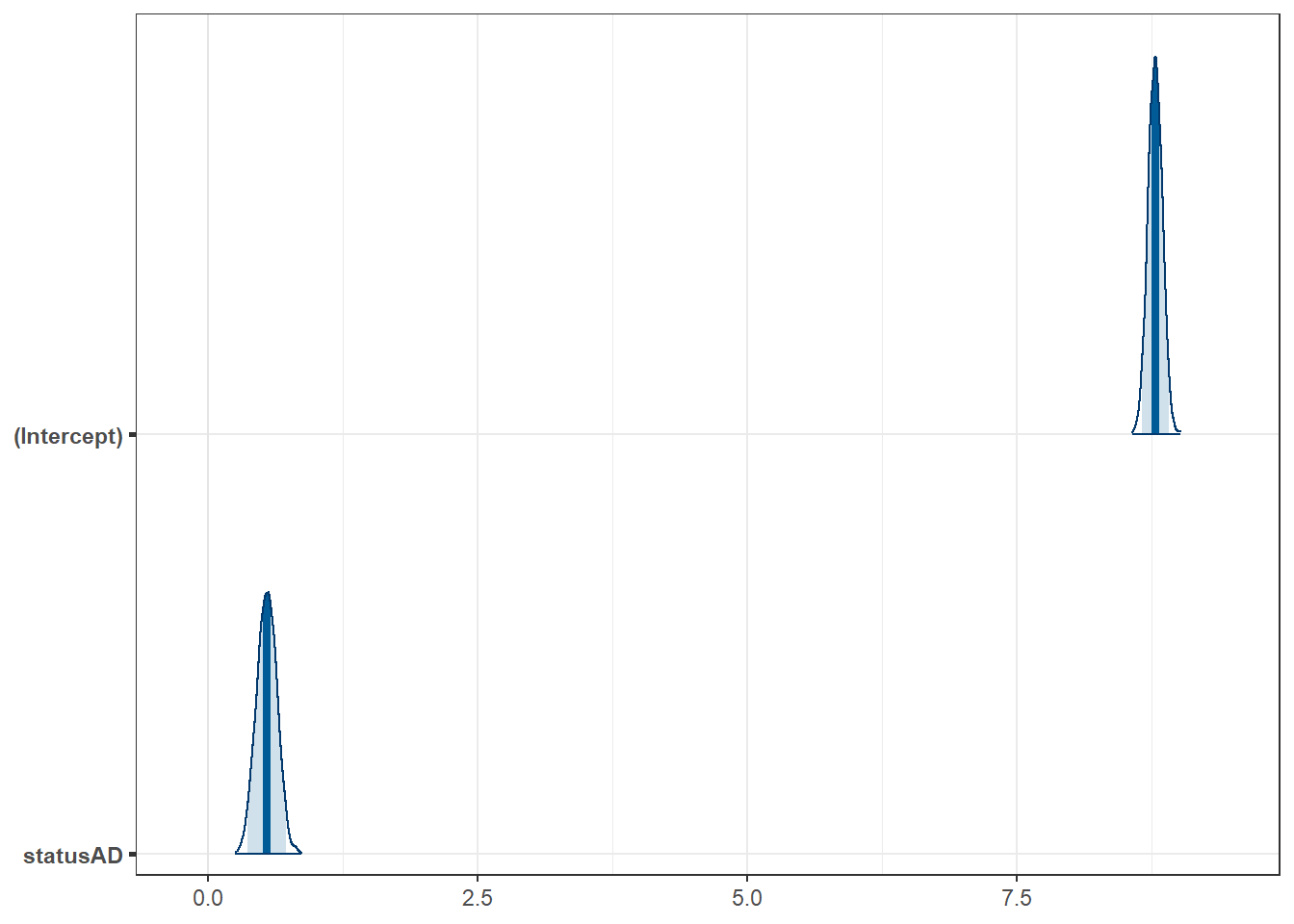
fit3 <- lm(logtime03 ~ status, data = darwin)

fit3 |> model_parameters(ci = 0.95) |>
  kable(digits = 2)
Parameter Coefficient SE CI CI_low CI_high t df_error p
(Intercept) 8.78 0.07 0.95 8.65 8.91 133.37 172 0
statusAD 0.55 0.09 0.95 0.36 0.73 5.92 172 0 
estimate_contrasts(fit3, ci = 0.95, contrast = "status")
Marginal Contrasts Analysis

Level1 | Level2 | Difference |         95% CI |   SE | t(172) |      p
----------------------------------------------------------------------
HC     |     AD |      -0.55 | [-0.73, -0.36] | 0.09 |  -5.92 | < .001

Marginal contrasts estimated at status
p-value adjustment method: Holm (1979)

The AD group has a higher (log time) by about 0.55 with a 95% uncertainty interval of (0.36, 0.73). This transformed time value is no longer expressed in milliseconds, of course, since we’re now talking about a logarithm of time, rather than our original Task 3 time.

7.8.1 Back-transforming the model’s predictions

Your model holds in the “transformed data” world. We cannot back-transform the regression coefficients in a rational way.

After fitting a model, it is useful to generate model-based estimates of the outcomes for different combinations of predictor values, and we can back-transform these predictions to get back to our original scale, as follows.

7.8.1.1 Predictions for The Average Across Many Subjects

If we consider the entire HC group, we would predict that the average log(time03) would be what, exactly?

estimate_expectation(fit3, data = "grid", ci = 0.95) 
Model-based Expectation

status | Predicted |   SE |       95% CI
----------------------------------------
HC     |      8.78 | 0.07 | [8.65, 8.91]
AD     |      9.33 | 0.06 | [9.20, 9.46]

Variable predicted: logtime03
Predictors modulated: status

The model fit3 and the estimate_expectation() function can be used to generate expectations for logtime03, which we can then exponentiate to obtain…

  • our expectation in terms of the average time to complete Task 3 in milliseconds across all HC subjects, which is 6502 ms (exp(8.78)), with 95% uncertainty interval (5710, 7406) (from exp(8.65), exp(8.91).)
Using R as a calculator

Here, we use R as a calculator…

round_half_up(exp(c(8.78, 8.65, 8.91)),0)
[1] 6503 5710 7406

Note that the round_half_up() function comes from the janitor package and is an effective way of rounding results for presentation. More on this function is available on the janitor reference page.

  • our expectation in terms of the average time to complete Task 3 in milliseconds across all AD subjects turns out to be 11271 ms, with 95% uncertainty interval (9897, 12836).
Again, using R as a calculator 
round_half_up(exp(c(9.33, 9.20, 9.46)),0)
[1] 11271  9897 12836

7.8.1.2 Predictions for Individual Subjects

We can also make predictions for individual subjects with HC or AD, using the estimate_prediction() function applied to our regression model fit3.

estimate_prediction(fit3, data = "grid", ci = 0.95) 
Model-based Prediction

status | Predicted |   SE |        95% CI
-----------------------------------------
HC     |      8.78 | 0.61 | [7.58,  9.99]
AD     |      9.33 | 0.61 | [8.12, 10.53]

Variable predicted: logtime03
Predictors modulated: status
  • our prediction of the time an individual HC subject would need to complete Task 3 (in milliseconds) turns out to be 6503 ms, with 95% uncertainty interval (1959, 21807).
round_half_up(exp(c(8.78, 7.58, 9.99)),0)
[1]  6503  1959 21807
  • our prediction of the time an individual AD subject would need to complete Task 3 (in milliseconds) turns out to be 11271 ms, with 95% uncertainty interval (3361, 37421).
round_half_up(exp(c(9.33, 8.12, 10.53)),0)
[1] 11271  3361 37421

Note how much wider the uncertainty intervals are for individual subjects than for the average across all subjects with a certain status (HC or AD.)

7.8.2 Bootstrap CI for Linear Model Coefficients

Rather than using an OLS fit to obtain the t-distribution based confidence interval for our linear model, we could also bootstrap the confidence intervals in this model with …

model_parameters(fit3, bootstrap = TRUE, iterations = 2000,
  ci = 0.95, centrality = "median", ci_method = "quantile")
Parameter   | Coefficient |       95% CI |      p
-------------------------------------------------
(Intercept) |        8.78 | [8.66, 8.90] | < .001
status [AD] |        0.55 | [0.38, 0.73] | < .001

Uncertainty intervals (equal-tailed) are naıve bootstrap intervals.

7.9 Other approaches

7.9.1 t test (Welch - not pooling SD)

If we run R’s default t test, without assuming equal population variances, on our logged times, we obtain the following, and we’ll also add a calculation of a standardized difference (Cohen’s d) for the effect size (difference in means on the log scale).

fit3a <- t.test(logtime03 ~ status, data = darwin)

fit3a |> model_parameters(ci = 0.95)
Welch Two Sample t-test

Parameter |  Group | status = HC | status = AD | Difference |         95% CI | t(169.24) |      p
-------------------------------------------------------------------------------------------------
logtime03 | status |        8.78 |        9.33 |      -0.55 | [-0.73, -0.36] |     -5.94 | < .001

Alternative hypothesis: true difference in means between group HC and group AD is not equal to 0
cohens_d(logtime03 ~ status, data = darwin, pooled_sd = FALSE)
Cohen's d |         95% CI
--------------------------
-0.90     | [-1.21, -0.59]

- Estimated using un-pooled SD.

7.9.2 t test (with pooled SD)

The t test on our logged times assuming equal variances in the two groups produces the same result as our linear model fit with lm(), of course. Here, though, we can also add a calculation of a standardized difference for the effect size on the log scale.

fit3b <- t.test(logtime03 ~ status, data = darwin, var.equal = TRUE)

fit3b |> model_parameters(ci = 0.95)
Two Sample t-test

Parameter |  Group | status = HC | status = AD | Difference |         95% CI | t(172) |      p
----------------------------------------------------------------------------------------------
logtime03 | status |        8.78 |        9.33 |      -0.55 | [-0.73, -0.36] |  -5.92 | < .001

Alternative hypothesis: true difference in means between group HC and group AD is not equal to 0
cohens_d(logtime03 ~ status, data = darwin, pooled_sd = TRUE)
Cohen's d |         95% CI
--------------------------
-0.90     | [-1.21, -0.58]

- Estimated using pooled SD.

Because the two groups (HC and AD) have very similar sample sizes and, after transformation, similar standard deviations (and thus similar variances, since the variance is just the square of the standard deviation), it really doesn’t matter whether or not we assume equal variances for these data.

7.9.3 Wilcoxon Signed Rank

We could, instead of transforming the data with the logarithm, use a non-parametric approach to compare the distributions (although this doesn’t compare the means) such as a Wilcoxon signed rank test.

wilcox.test(time03 ~ status, data = darwin, 
            conf.int = TRUE, conf.level = 0.95)

    Wilcoxon rank sum test with continuity correction

data:  time03 by status
W = 1829, p-value = 4.105e-09
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
 -6730 -3190
sample estimates:
difference in location 
                 -4950

7.9.4 Bayesian linear model

We could also fit a Bayesian linear model to our logged times for Task 3, as follows:

set.seed(431)
fit3c <- stan_glm(logtime03 ~ status, data = darwin, refresh = 0)

post3c <- describe_posterior(fit3c, ci = 0.95)

print_md(post3c, digits = 2)
Summary of Posterior Distribution
Parameter Median 95% CI pd ROPE % in ROPE Rhat ESS
(Intercept) 8.78 [8.66, 8.91] 100% [-0.07, 0.07] 0% 1.000 3621.00
statusAD 0.55 [0.36, 0.72] 100% [-0.07, 0.07] 0% 0.999 3435.00 
plot(fit3c, plotfun = "areas", prob = 0.95, 
     pars = c("(Intercept)", "statusAD"))

fit3c |> model_parameters() |> kable(digits = 2)
Parameter Median CI CI_low CI_high pd Rhat ESS Prior_Distribution Prior_Location Prior_Scale
(Intercept) 8.78 0.95 8.66 8.91 1 1 3620.57 normal 9.06 1.66
statusAD 0.55 0.95 0.36 0.72 1 1 3435.02 normal 0.00 3.31

As with an OLS model fit with lm(), we can back-transform expectations or predictions from this model, but not the coefficients themselves.

estimate_expectation(fit3c, data = "grid", ci = 0.95)
Model-based Expectation

status | Predicted |   SE |       95% CI
----------------------------------------
HC     |      8.78 | 0.07 | [8.66, 8.91]
AD     |      9.33 | 0.07 | [9.20, 9.46]

Variable predicted: logtime03
Predictors modulated: status
round_half_up(exp(c(8.78, 8.66, 8.91)),0) # for the mean across HC subjects
[1] 6503 5768 7406
round_half_up(exp(c(9.33, 9.20, 9.46)),0) # for the mean across AD subjects
[1] 11271  9897 12836
estimate_prediction(fit3c, data = "grid", ci = 0.95)
Model-based Prediction

status | Predicted |   SE |        95% CI
-----------------------------------------
HC     |      8.79 | 0.60 | [7.58,  9.97]
AD     |      9.33 | 0.61 | [8.13, 10.52]

Variable predicted: logtime03
Predictors modulated: status
round_half_up(exp(c(8.79, 7.58, 10.03)),0) # for an individual HC subject
[1]  6568  1959 22697
round_half_up(exp(c(9.32, 8.12, 10.56)),0) # for an individual AD subject
[1] 11159  3361 38561

7.9.5 Bootstrap CI for mean (time03) without transformation

Finally, we could use the bootstrap directly to build a confidence interval around the difference in means, without using a transformation. The first way I’ll do this uses the tools from the infer package.

set.seed(431)
darwin |>
  specify(time03 ~ status) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate( stat = "diff in means", order = c("AD", "HC") ) |>
  get_confidence_interval( level = 0.95, type = "percentile" )
# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1    4270.    8048.

Or we could use the boot.t.test() approach from the MKinfer package.

set.seed(431)
boot.t.test(time03 ~ status, var.equal = TRUE, R = 2000,
  data = darwin, conf.level = 0.95)

    Bootstrap Two Sample t-test

data:  time03 by status
number of bootstrap samples:  2000
bootstrap p-value < 5e-04 
bootstrap difference of means (SE) = -6115.905 (1087.369) 
95 percent bootstrap percentile confidence interval:
 -8236.120 -3963.146

Results without bootstrap:
t = -6.1265, df = 172, p-value = 5.94e-09
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -8081.771 -4143.116
sample estimates:
mean in group HC mean in group AD 
        7476.882        13589.326

Note the difference between the raw t test result (results without bootstrap) and the bootstrap in this setting.

We can run this without assuming equal population variances, as well.

set.seed(431)
boot.t.test(time03 ~ status, var.equal = FALSE, R = 2000,
  data = darwin, conf.level = 0.95 )

    Bootstrap Welch Two Sample t-test

data:  time03 by status
number of bootstrap samples:  2000
bootstrap p-value < 5e-04 
bootstrap difference of means (SE) = -6130.079 (977.7301) 
95 percent bootstrap percentile confidence interval:
 -8147.991 -4226.181

Results without bootstrap:
t = -6.2074, df = 134.42, p-value = 6.245e-09
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -8059.950 -4164.937
sample estimates:
mean in group HC mean in group AD 
        7476.882        13589.326

7.9.6 Bootstrap CI for Medians

Instead of comparing mean times to complete Task 3, we could use the bootstrap to compare the medians directly.

set.seed(431)
darwin |>
  specify(time03 ~ status) |>
  generate(reps = 2500, type = "bootstrap") |>
  calculate(
    stat = "diff in medians",
    order = c("AD", "HC")
  ) |>
  get_ci(level = 0.95, type = "percentile")
# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     3275    7522.

7.10 What about Task 1?

ggplot(darwin, aes(x = status, y = time01)) +
  geom_boxplot()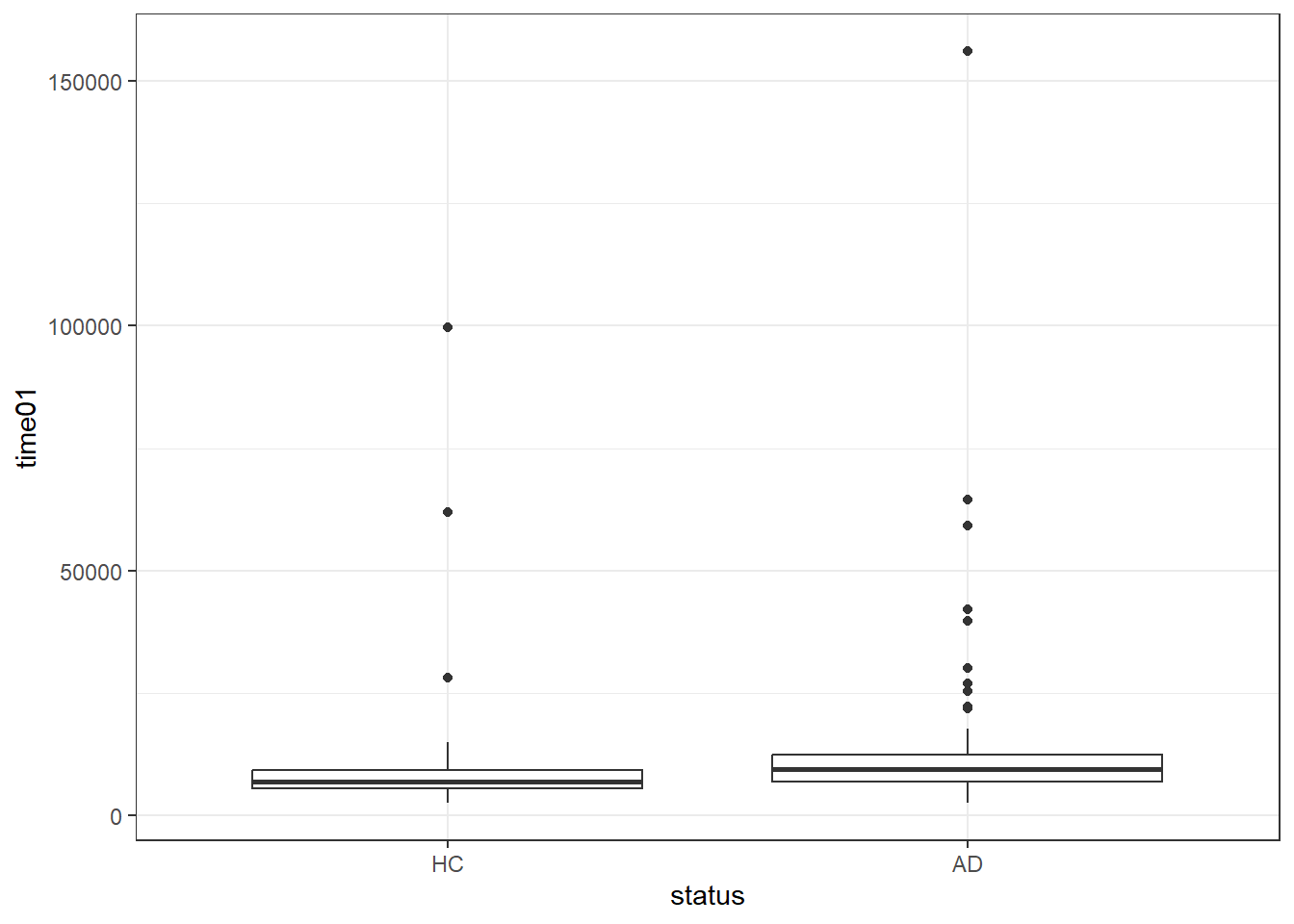

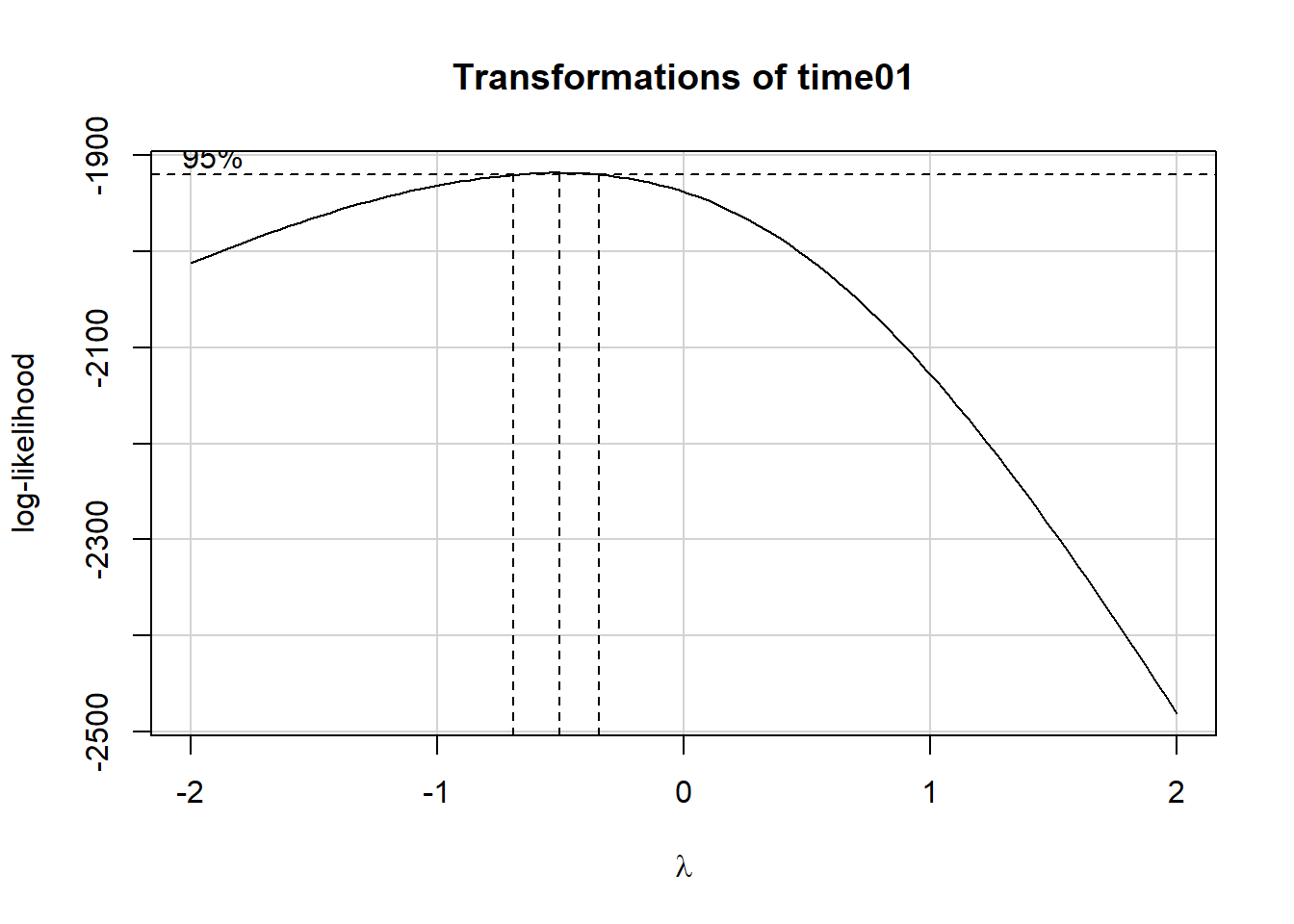
fit1 <- lm(time01 ~ status, data = darwin)
boxCox(fit1, main = "Transformations of time01")

summary(powerTransform(fit1))$result
    Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Y1 -0.5110717        -0.5   -0.6849666   -0.3371769
ggplot(darwin, aes(x = status, y = (time01^-0.5))) +
  geom_boxplot()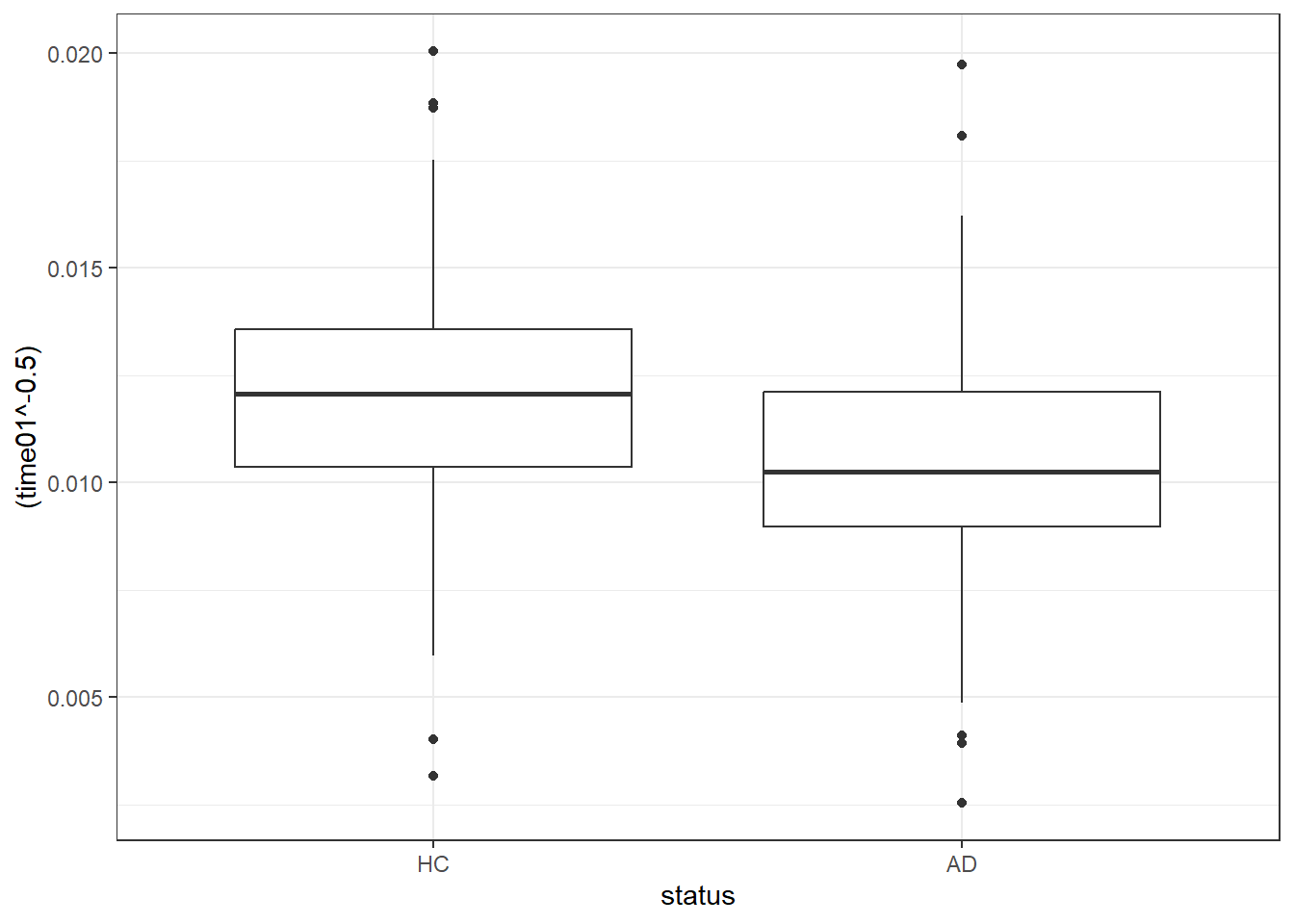

darwin <- darwin |>
  mutate(trans_t01 = 1000 * time01^(-0.5))

darwin |>
  reframe(lovedist(trans_t01), .by = status)
# A tibble: 2 × 11
  status     n  miss  mean    sd   med   mad   min   q25   q75   max
  <fct>  <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 HC        85     0  12.0  2.81  12.1  2.37  3.17 10.4   13.6  20.0
2 AD        89     0  10.5  3.05  10.2  2.02  2.53  8.97  12.1  19.7

7.10.1 Linear Model

fit1 <- lm(trans_t01 ~ status, data = darwin)

fit1 |>
  model_parameters(ci = 0.95) |>
  kable(digits = 2)
Parameter Coefficient SE CI CI_low CI_high t df_error p
(Intercept) 11.98 0.32 0.95 11.36 12.61 37.64 172 0
statusAD -1.45 0.45 0.95 -2.33 -0.57 -3.25 172 0 
estimate_contrasts(fit1, ci = 0.95, contrast = "status")
Marginal Contrasts Analysis

Level1 | Level2 | Difference |       95% CI |   SE | t(172) |     p
-------------------------------------------------------------------
HC     |     AD |       1.45 | [0.57, 2.33] | 0.45 |   3.25 | 0.001

Marginal contrasts estimated at status
p-value adjustment method: Holm (1979)

7.10.2 Back-transformation of predictions and expectations…

Here our transformation is trans_t01 = 1000 * time01^(-0.5). To back out of this transformation, we need to do a little algebra…

\[ trans_{t01} = 1000 * time01^{-0.5} \\ trans_{t01} = 1000 * \left(\frac{1}{\sqrt{time01}}\right) \\ \frac{trans_{t01}}{1000} = \left(\frac{1}{\sqrt{time01}}\right) \\ \frac{1000}{trans_{t01}} = \sqrt{time01} \\ \left(\frac{1000}{trans_{t01}}\right)^2 = time01 \]

We can obtain an expectation for trans_t01 from estimate_expectation() and then apply this transformation in order to describe the result in terms of the time to complete Task 1 in milliseconds, as follows…

estimate_expectation(fit1, data = "grid", ci = 0.95)
Model-based Expectation

status | Predicted |   SE |         95% CI
------------------------------------------
HC     |     11.98 | 0.32 | [11.36, 12.61]
AD     |     10.54 | 0.31 | [ 9.92, 11.15]

Variable predicted: trans_t01
Predictors modulated: status

So, for example, our expectation for the average across all HC subjects is 11.98 after our transformation. Backing out of this transformation, we have an estimate of 6968 milliseconds.

round_half_up((1000 / 11.98)^2, 0)
[1] 6968

To obtain the uncertainty interval for the expectation across all HC subjects, we apply the back-transformation to the endpoints of the interval, and then round the results to no decimal places as follows:

round_half_up(c((1000 / 10.54)^2, (1000 / 9.92)^2, (1000 / 11.15)^2), 0)
[1]  9002 10162  8044

and so our model’s estimate for the time spent on Task 1 for HC subjects on average is 6968 milliseconds, with a 95% uncertainty interval of (6289, 7749) milliseconds.

For the average across AD subjects, we have a point estimate for the time spent on Task 1 of 9002 ms, and a 95% uncertainty interval of (8044, 10162) ms.

round_half_up(c((1000 / 11.36)^2, (1000 / 12.61)^2), 0)
[1] 7749 6289

We can obtain analogous results for individual predictions for HC and AD subjects, respectively, according to this model for transformed Task 1 times, with the following code:

estimate_prediction(fit1, data = "grid", ci = 0.95)
Model-based Prediction

status | Predicted |   SE |        95% CI
-----------------------------------------
HC     |     11.98 | 2.95 | [6.16, 17.81]
AD     |     10.54 | 2.95 | [4.71, 16.36]

Variable predicted: trans_t01
Predictors modulated: status
round_half_up(c((1000 / 11.98)^2, (1000 / 6.16)^2, (1000 / 17.81)^2), 0) ## HC subjects
[1]  6968 26354  3153
round_half_up(c((1000 / 10.54)^2, (1000 / 4.71)^2, (1000 / 16.36)^2), 0) ## AD subjects
[1]  9002 45077  3736

All of our other approaches used for Task 3 would also work for Task 1, certainly.

7.11 What about Task 25?

Finally, let’s consider Task 25.

ggplot(darwin, aes(x = status, y = time25)) +
  geom_boxplot()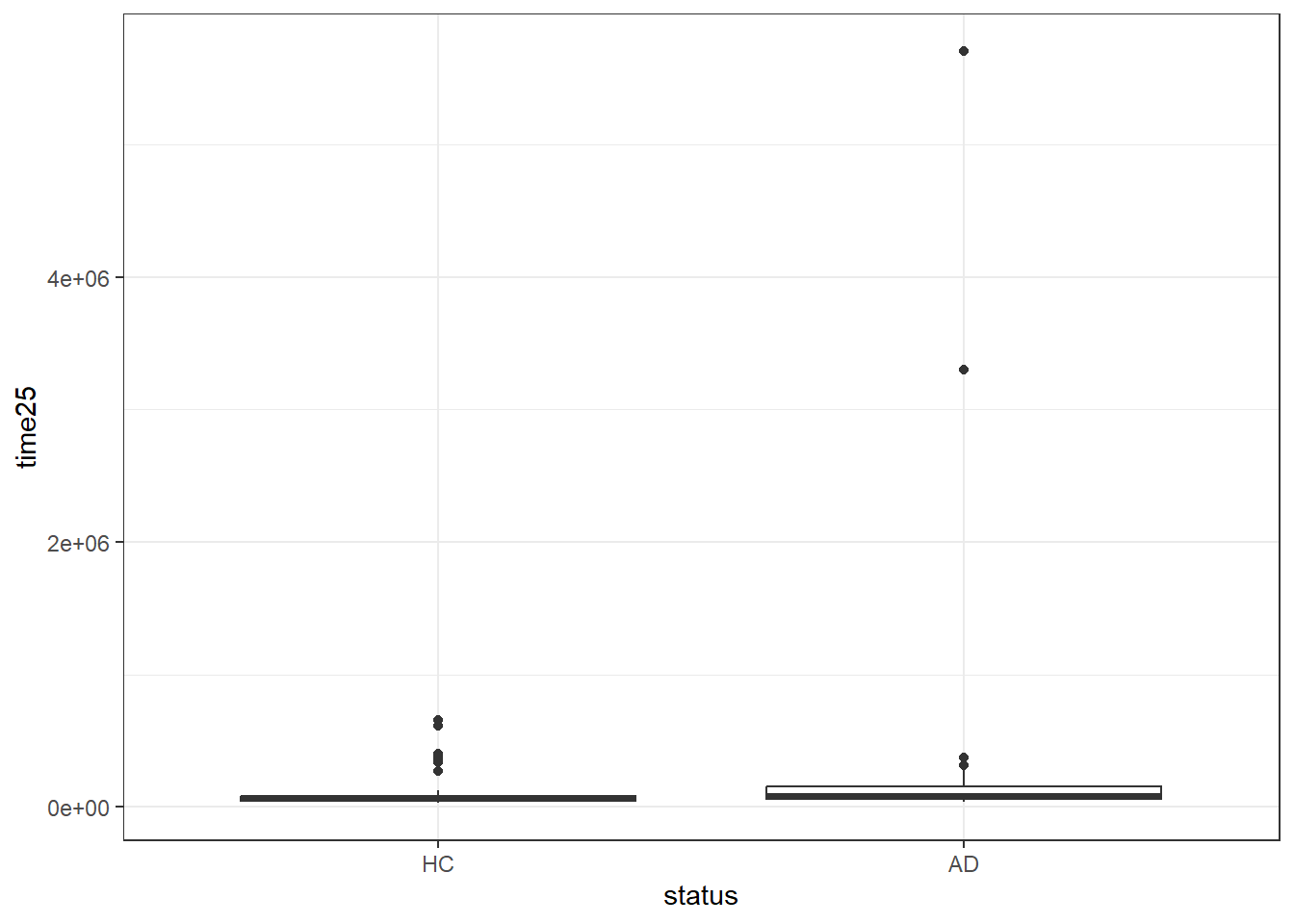

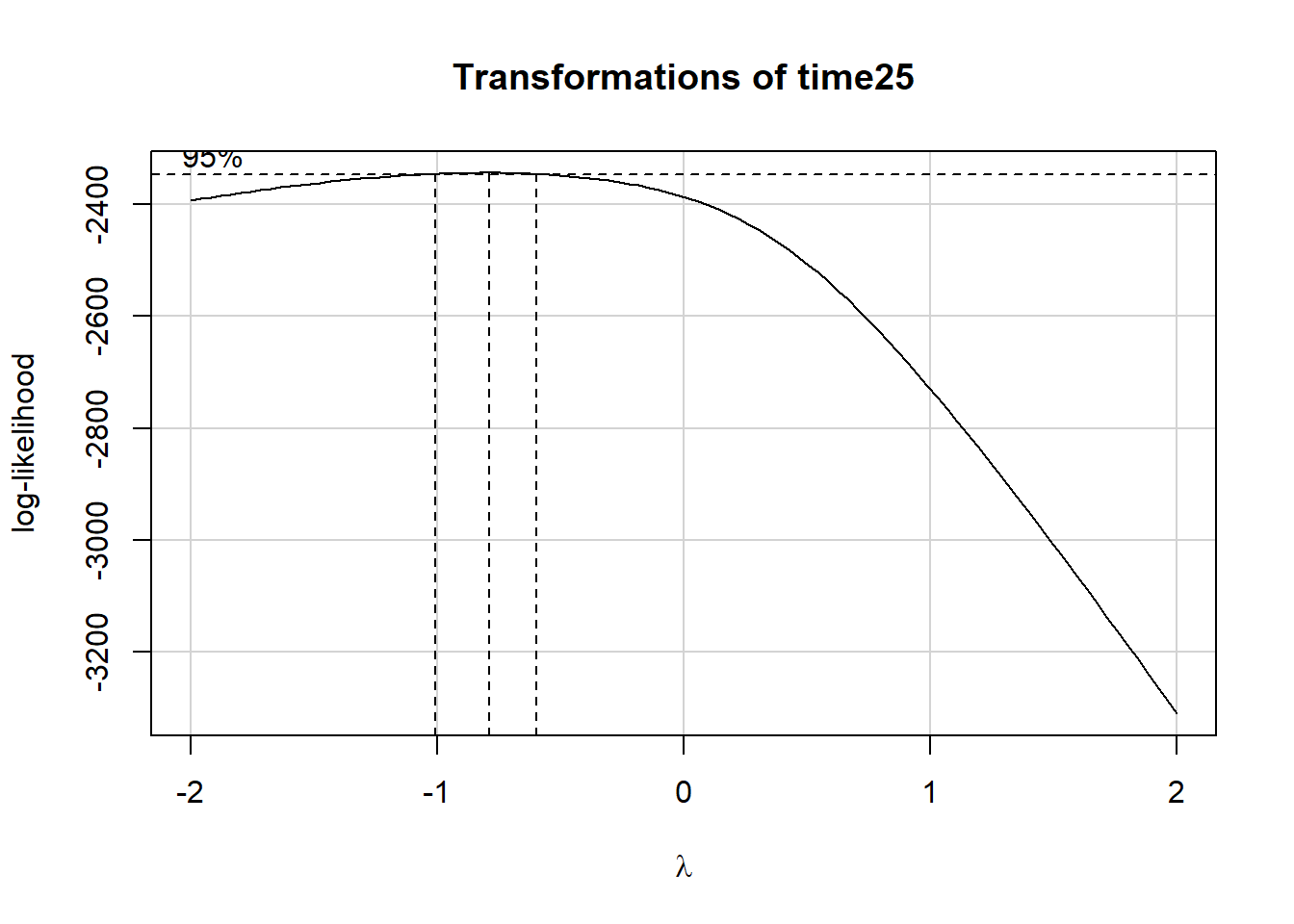
fit25 <- lm(time25 ~ status, data = darwin)
boxCox(fit25, main = "Transformations of time25")

summary(powerTransform(fit25))$result
    Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Y1 -0.7965846          -1    -1.002999   -0.5901699

Now, we’ll use an inverse transformation and also multiply the values by 1,000,000 in order to get coefficients which fall between 1 and 100.

ggplot(darwin, aes(x = status, y = (1000000 / time25))) +
  geom_boxplot()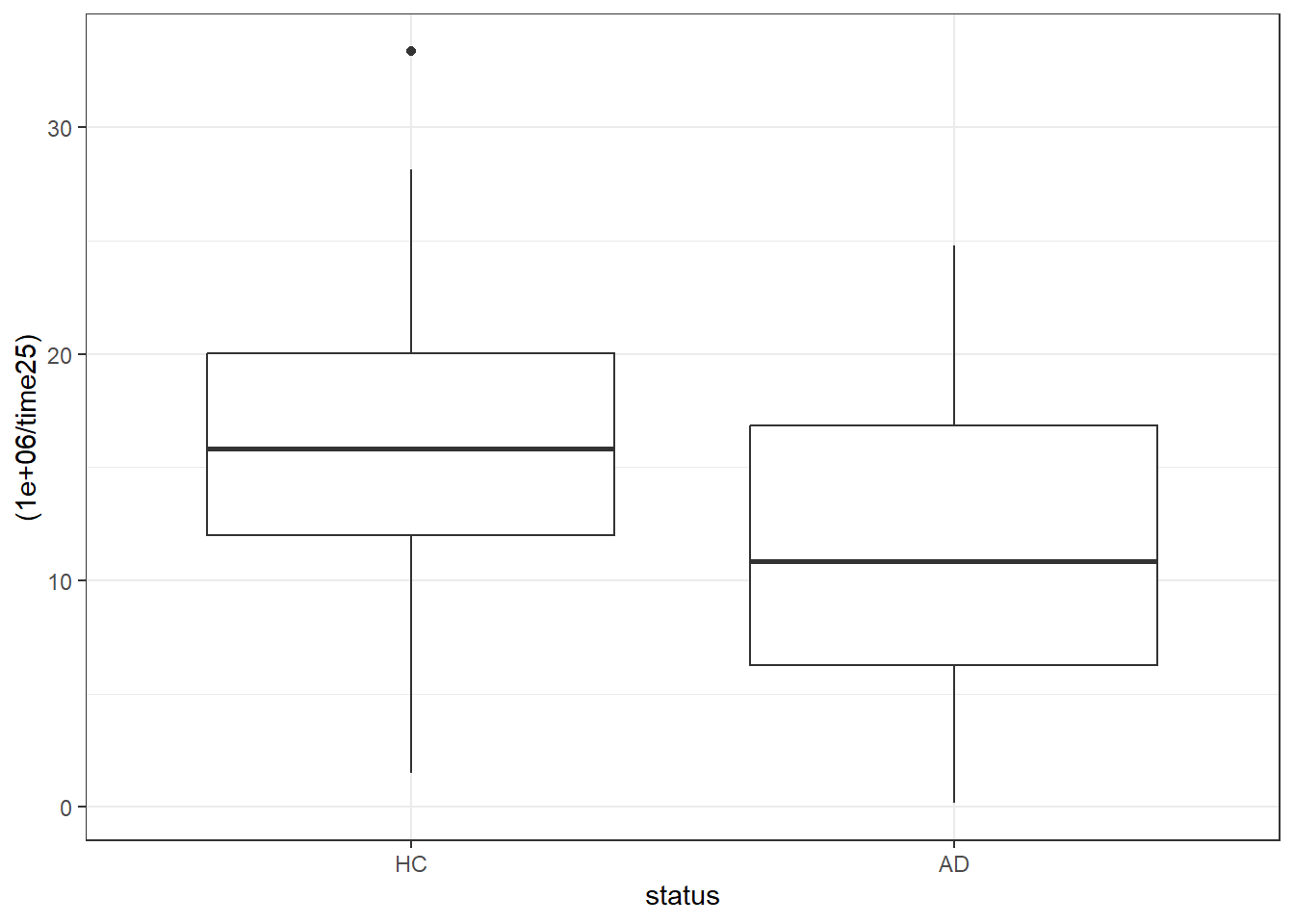

darwin <- darwin |>
  mutate(trans_t25 = 1000000 / time25)

darwin |>
  reframe(lovedist(trans_t25), .by = status)
# A tibble: 2 × 11
  status     n  miss  mean    sd   med   mad   min   q25   q75   max
  <fct>  <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 HC        85     0  15.3  6.84  15.8  5.74 1.52  12.0   20.0  33.4
2 AD        89     0  11.0  5.68  10.9  7.19 0.175  6.27  16.8  24.8

7.11.1 Linear Model

fit25 <- lm(trans_t25 ~ status, data = darwin)

fit25 |> model_parameters(ci = 0.95) |> kable(digits = 2)
Parameter Coefficient SE CI CI_low CI_high t df_error p
(Intercept) 15.25 0.68 0.95 13.91 16.59 22.41 172 0
statusAD -4.27 0.95 0.95 -6.15 -2.40 -4.49 172 0 
estimate_contrasts(fit25, ci = 0.95, contrast = "status")
Marginal Contrasts Analysis

Level1 | Level2 | Difference |       95% CI |   SE | t(172) |      p
--------------------------------------------------------------------
HC     |     AD |       4.27 | [2.40, 6.15] | 0.95 |   4.49 | < .001

Marginal contrasts estimated at status
p-value adjustment method: Holm (1979)

We could also bootstrap the confidence intervals in this model with …

model_parameters(fit25, bootstrap = TRUE, iterations = 2000,
  ci = 0.95, centrality = "median", ci_method = "quantile")
Parameter   | Coefficient |         95% CI |      p
---------------------------------------------------
(Intercept) |       15.26 | [13.79, 16.68] | < .001
status [AD] |       -4.28 | [-6.16, -2.31] | < .001

Uncertainty intervals (equal-tailed) are naıve bootstrap intervals.

Working with the original lm() fit, we can obtain predictions or expectations and back-transform them as before. I’ll show the average expectations here…

estimate_expectation(fit25, data = "grid", ci = 0.95)
Model-based Expectation

status | Predicted |   SE |         95% CI
------------------------------------------
HC     |     15.25 | 0.68 | [13.91, 16.59]
AD     |     10.98 | 0.67 | [ 9.67, 12.29]

Variable predicted: trans_t25
Predictors modulated: status

Here are the back-transformed point estimate and 95% uncertainty interval for an individual prediction for a subject with status AD to complete Task 25, in milliseconds…

round_half_up(c((1000000 / 10.98), (1000000 / 9.67), (1000000 / 12.29)),0)
[1]  91075 103413  81367

so the point estimate is 91075 ms, with 95% uncertainty interval (81367, 103413).

However, we run into a challenge when we look at transforming out of the uncertainty interval for individual predictions.

estimate_prediction(fit25, data = "grid", ci = 0.95)
Model-based Prediction

status | Predicted |   SE |         95% CI
------------------------------------------
HC     |     15.25 | 6.31 | [ 2.80, 27.71]
AD     |     10.98 | 6.31 | [-1.48, 23.43]

Variable predicted: trans_t25
Predictors modulated: status

For an individual AD subject, we have:

round_half_up(c((1000000 / 10.98), (1000000 / -1.48), (1000000 / 23.43)),0)
[1]   91075 -675676   42680

Our 95% uncertainty interval now includes negative times, and the uncertainty interval no longer includes the point estimate, and this causes multiple problems. This suggests that transforming our way out of a problem when making a comparison of this sort is not always going to produce useful results.

7.12 For More Information

  1. Transformation is discussed in some detail as part of this vignette for the modelbased package vignette from the easystats meta-package.

  2. You can learn more about model-based response estimates and uncertainty at this link which describes both the estimate_expection() and estimate_prediction() functions.

  3. More on the Box-Cox family of power transformations and how they are used in R is available in this post from 2022 at Data Science Tutorials. A more general discussion of power transforms, including Box-Cox is available through Wikipedia.

  4. Another nice introduction to transformations (using Stata, rather than R, but the ideas are still relevant) is available here.

  5. This overview of functions in the janitor package includes explanations for several useful tools, including the round_half_up() function.